03. 2D histograms and density plots

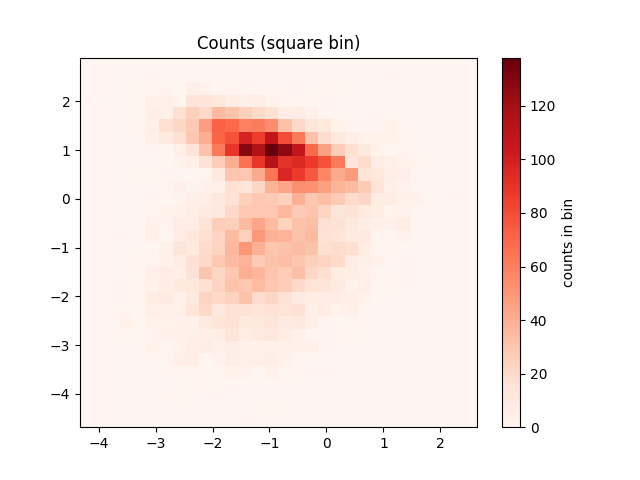
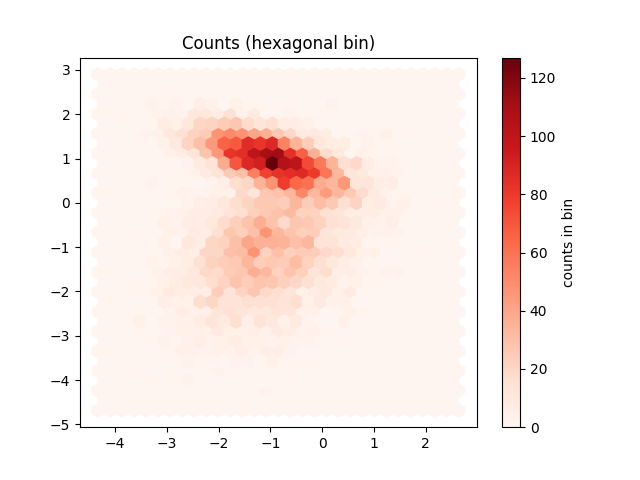
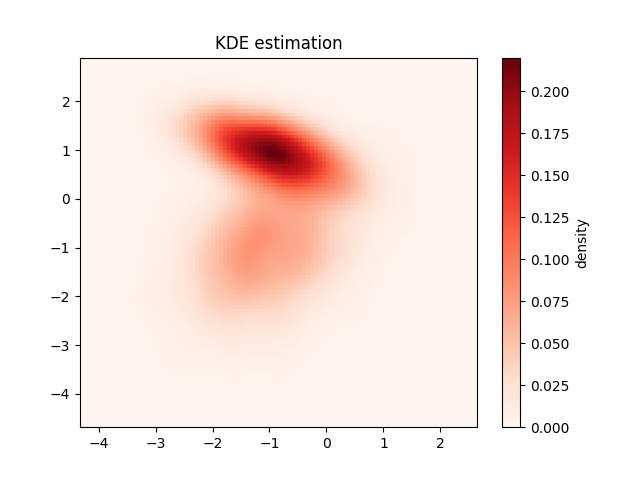
This script demonstrates three techniques for visualizing the density of a large 2D dataset, which helps to avoid overplotting in standard scatter plots. It compares:

• plt.hist2d for square binning.

• plt.hexbin for hexagonal binning.

• A smooth density plot using Kernel Density Estimation (KDE).

See: https://jakevdp.github.io/PythonDataScienceHandbook/04.05-histograms-and-binnings.html

• 
• 
• 

Out:

C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\matplotlib\plot_main03_hist2d.py:86: UserWarning:

FigureCanvasAgg is non-interactive, and thus cannot be shown

# Libraries
import numpy as np
import matplotlib.pyplot as plt

# Specific library
from sklearn.datasets import make_blobs
from sklearn.datasets import make_classification
from scipy.stats import gaussian_kde

# ----------------------------
# Load data
# ----------------------------
# Create data
mean = [0, 0]
cov = [[1, 1], [1, 2]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T

# Create data
data, t = make_classification(n_samples=8000, n_features=2,
    n_informative=2, n_redundant=0, n_repeated=0, n_classes=2,
    n_clusters_per_class=1, weights=None, flip_y=0.00,
    class_sep=1.0, hypercube=True, shift=0.0, scale=1.0,
    shuffle=True, random_state=32)
x, y = data[:,0], data[:,1]


# ----------------------------
# Visualize
# ----------------------------
# Plot hist
f1 = plt.hist2d(x, y, bins=30, cmap='Reds')
cb = plt.colorbar()
cb.set_label('counts in bin')
plt.title('Counts (square bin)')

# Plot hex
plt.figure()
f2 = plt.hexbin(x, y, gridsize=30, cmap='Reds')
cb = plt.colorbar()
cb.set_label('counts in bin')
plt.title('Counts (hexagonal bin)')

# Plot density
data = np.vstack([x, y])
kde = gaussian_kde(data)

# Parameters
xmin, xmax = min(x), max(x)
ymin, ymax = min(y), max(y)

# evaluate on a regular grid
xgrid = np.linspace(xmin, xmax, 100)
ygrid = np.linspace(ymin, ymax, 100)
Xgrid, Ygrid = np.meshgrid(xgrid, ygrid)
Z = kde.evaluate(np.vstack([
    Xgrid.ravel(),
    Ygrid.ravel()
]))

# Plot the result as an image
plt.figure()
plt.imshow(Z.reshape(Xgrid.shape),
           origin='lower', aspect='auto',
           extent=[xmin, xmax, ymin, ymax],
           cmap='Reds')
cb = plt.colorbar()
cb.set_label("density")
plt.title("KDE estimation")

# Show
plt.show()