pyamr.core.regression.wls pyamr.core.regression.wls ========================= =========================
Classes
- class pyamr.core.regression.wls.PredictionResult(mean, cilo, ciup, pstd, pilo, piup, time, nobs, endog)[source]
- class pyamr.core.regression.wls.WLSWrapper(estimator=None, evaluate=True)[source]
The description…
Methods:
as_summary(**kwargs)This method creates a summary string.
evaluate([alpha])This method set all the variables into this class.
fit(endog[, exog, trend, weights, W])This method computes the WLS.
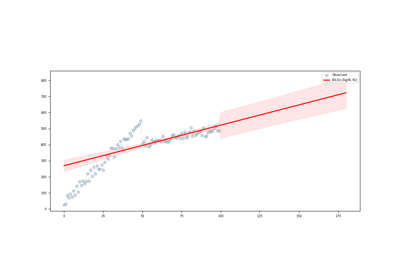
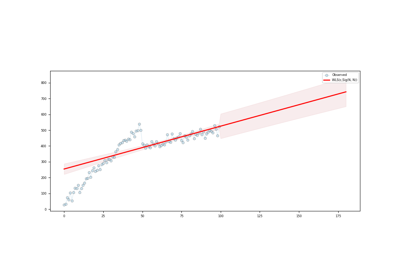
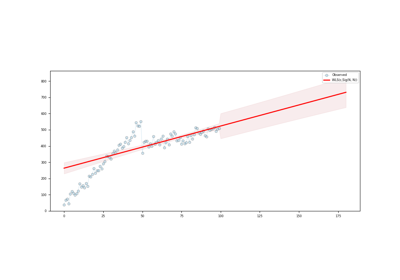
get_prediction([start, end, alpha])This method predicts using the model.
line(x)This method returns arrays to plot line and confidence intervals.
pred_int([start, end])This method computes the prediction intervals
- evaluate(alpha=0.05)[source]
This method set all the variables into this class.
- Notes:
if instead of having the attribute series it is desired to set each element of the series as an attribute, just used the following statement: setattr(self, name, value).
Note the difference between the resid and wresid since they will also have different statistical properties. Furthermore, there is a vector with normalized residuals resid_pearson.
@see: statsmodels.WLS @see: pyAMR.core.regression.RegressionResultsWrapper
- Parameters:
alpha (the confidence interval)
- Returns:
dictionary
- Return type:
map with all the parameters.
- fit(endog, exog=None, trend='n', weights=None, W=None, **kwargs)[source]
This method computes the WLS.
@see statsmodels.regression.linear_model.WLS
- Parameters:
endog (array-like) – The endogenous variable (aka. time series data)
exog (array-like) – The exogenous variable (by default is the time t starting in 0)
trend (str-like, options = {c, n}) – Wether to add a constant or not.
weights (array-like (optional)) – The weights for the weighted least square regression. If weights and W are both not None, the W instance will be used to transform the weights variables.
W (object-like (optional)) – The instance to transform the weights. It must implement the function ‘weights’.
kwargs (dict-like) – The rest of the arguments to pass to the __init__ and fit methods of the class statsmodels.WLS (see xxx)
- Returns:
object
- Return type:
OLSWrapper object.
- get_prediction(start=None, end=None, alpha=0.05, **kwargs)[source]
This method predicts using the model.
Todo
Note that wls_predict_std has weights (those used in WLS) as an input parameter. However, these are not passed to the function. Those weights are available for insample predictions but not for forecasting.
- Parameters:
start (int (optional)) – The time t to start the prediction
end (int (optional)) – The time t to end the prediction
kwargs – The arguments to pass to the method get_prediction of the class statsmodels.WLS (see xxx)
- Return type:
time, prediction mean, prediction confidence interval