Note
Go to the end to download the full example code
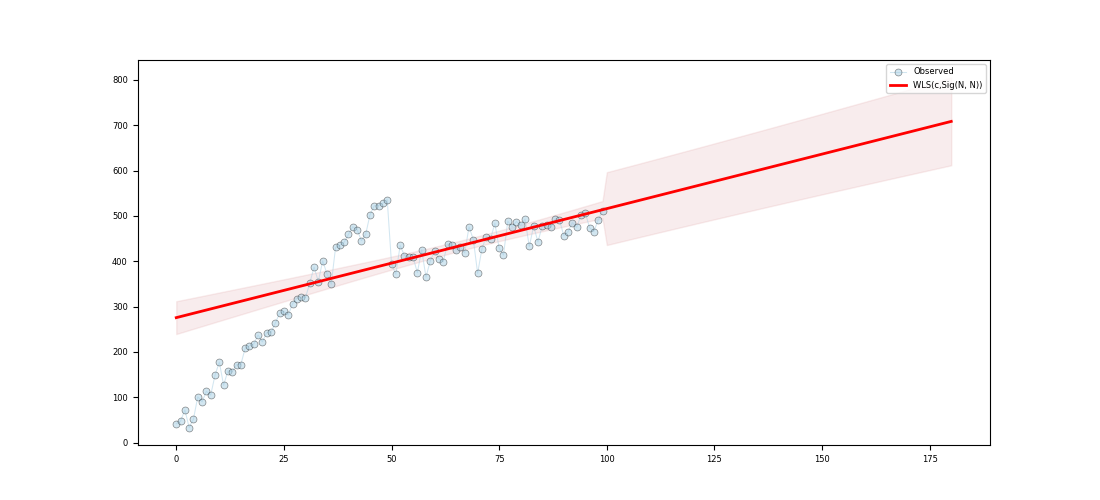
WLS - Basic
c:\users\kelda\desktop\repositories\virtualenvs\venv-py391-pyamr\lib\site-packages\statsmodels\regression\linear_model.py:807: RuntimeWarning:
divide by zero encountered in log
Series:
wls-rsquared 0.4773
wls-rsquared_adj 0.472
wls-fvalue 89.4894
wls-fprob 0.0
wls-aic inf
wls-bic inf
wls-llf -inf
wls-mse_model 137903.9406
wls-mse_resid 1541.008
wls-mse_total 2918.4114
wls-const_coef 275.6131
wls-const_std 18.2135
wls-const_tvalue 15.1324
wls-const_tprob 0.0
wls-const_cil 239.469
wls-const_ciu 311.7571
wls-x1_coef 2.405
wls-x1_std 0.2542
wls-x1_tvalue 9.4599
wls-x1_tprob 0.0
wls-x1_cil 1.9005
wls-x1_ciu 2.9095
wls-s_dw 0.488
wls-s_jb_value 7.949
wls-s_jb_prob 0.0188
wls-s_skew 0.566
wls-s_kurtosis 3.791
wls-s_omnibus_value 8.126
wls-s_omnibus_prob 0.017
wls-m_dw 0.1295
wls-m_jb_value 6.1737
wls-m_jb_prob 0.0456
wls-m_skew -0.5865
wls-m_kurtosis 3.325
wls-m_nm_value 6.6625
wls-m_nm_prob 0.0357
wls-m_ks_value 0.5736
wls-m_ks_prob 0.0
wls-m_shp_value 0.9415
wls-m_shp_prob 0.0002
wls-m_ad_value 2.4991
wls-m_ad_nnorm False
wls-missing raise
wls-exog [[1.0, 0.0...
wls-endog [41.719565...
wls-trend c
wls-weights [0.0435648...
wls-W <pyamr.met...
wls-model <statsmode...
wls-id WLS(c,Sig(...
dtype: object
Regression line:
[275.61 278.02 280.42 282.83 285.23 287.64 290.04 292.45 294.85 297.26]
Summary:
WLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.477
Model: WLS Adj. R-squared: 0.472
Method: Least Squares F-statistic: 89.49
Date: Thu, 15 Jun 2023 Prob (F-statistic): 1.80e-15
Time: 18:19:13 Log-Likelihood: -inf
No. Observations: 100 AIC: inf
Df Residuals: 98 BIC: inf
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 275.6131 18.213 15.132 0.000 239.469 311.757
x1 2.4050 0.254 9.460 0.000 1.900 2.910
==============================================================================
Omnibus: 8.126 Durbin-Watson: 0.488
Prob(Omnibus): 0.017 Jarque-Bera (JB): 7.949
Skew: 0.566 Prob(JB): 0.0188
Kurtosis: 3.791 Cond. No. 234.
Normal (N): 6.662 Prob(N): 0.036
==============================================================================
6 # Import class.
7 import sys
8 import numpy as np
9 import pandas as pd
10 import matplotlib as mpl
11 import matplotlib.pyplot as plt
12 import statsmodels.api as sm
13 import statsmodels.robust.norms as norms
14
15 # import weights.
16 from pyamr.datasets.load import make_timeseries
17 from pyamr.core.regression.wls import WLSWrapper
18 from pyamr.metrics.weights import SigmoidA
19
20 # ----------------------------
21 # set basic configuration
22 # ----------------------------
23 # Matplotlib options
24 mpl.rc('legend', fontsize=6)
25 mpl.rc('xtick', labelsize=6)
26 mpl.rc('ytick', labelsize=6)
27
28 # Set pandas configuration.
29 pd.set_option('display.max_colwidth', 14)
30 pd.set_option('display.width', 150)
31 pd.set_option('display.precision', 4)
32
33 # ----------------------------
34 # create data
35 # ----------------------------
36 # Create timeseries data
37 x, y, f = make_timeseries()
38
39 # Create method to compute weights from frequencies
40 W = SigmoidA(r=200, g=0.5, offset=0.0, scale=1.0)
41
42 # Note that the function fit will call M.weights(weights) inside and will
43 # store the M converter in the instance. Therefore, the code execute is
44 # equivalent to <weights=M.weights(f)> with the only difference being that
45 # the weight converter is not saved.
46 wls = WLSWrapper(estimator=sm.WLS).fit( \
47 exog=x, endog=y, trend='c', weights=f,
48 W=W, missing='raise')
49
50 # Print series.
51 print("\nSeries:")
52 print(wls.as_series())
53
54 # Print regression line.
55 print("\nRegression line:")
56 print(wls.line(np.arange(10)))
57
58 # Print summary.
59 print("\nSummary:")
60 print(wls.as_summary())
61
62 # -----------------
63 # Save & Load
64 # -----------------
65 # File location
66 #fname = '../../examples/saved/wls-sample.pickle'
67
68 # Save
69 #wls.save(fname=fname)
70
71 # Load
72 #wls = WLSWrapper().load(fname=fname)
73
74 # -------------
75 # Example I
76 # -------------
77 # This example shows how to make predictions using the wrapper and how
78 # to plot the resultin data. In addition, it compares the intervales
79 # provided by get_prediction (confidence intervals) and the intervals
80 # provided by wls_prediction_std (prediction intervals).
81 #
82 # To Do: Implement methods to compute CI and PI (see regression).
83
84 # Variables.
85 start, end = None, 180
86
87 # Compute predictions (exogenous?). It returns a 2D array
88 # where the rows contain the time (t), the mean, the lower
89 # and upper confidence (or prediction?) interval.
90 preds = wls.get_prediction(start=start, end=end)
91
92
93 # Create figure
94 fig, ax = plt.subplots(1, 1, figsize=(11,5))
95
96 # Plotting confidence intervals
97 # -----------------------------
98 # Plot truth values.
99 ax.plot(x, y, color='#A6CEE3', alpha=0.5, marker='o',
100 markeredgecolor='k', markeredgewidth=0.5,
101 markersize=5, linewidth=0.75, label='Observed')
102
103 # Plot forecasted values.
104 ax.plot(preds[0,:], preds[1, :], color='#FF0000', alpha=1.00,
105 linewidth=2.0, label=wls._identifier(short=True))
106
107 # Plot the confidence intervals.
108 ax.fill_between(preds[0, :], preds[2, :],
109 preds[3, :],
110 color='r',
111 alpha=0.1)
112
113 # Legend
114 plt.legend()
115
116 # Show
117 plt.show()
Total running time of the script: ( 0 minutes 0.114 seconds)