Note
Go to the end to download the full example code
Step 01 - Compute AMR metrics
Loading susceptibility test data
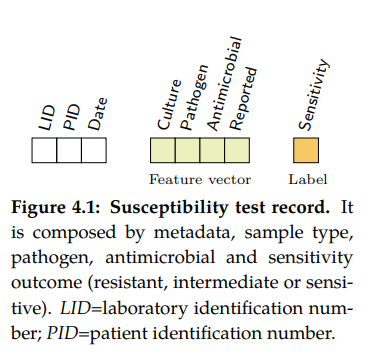
A Susceptibility test record (see figure 4.1) is composed by laboratory
identification number (LID), patient identification number (PID), date, sample
type, specimen or culture (e.g. blood or urine), pathogen, antimicrobial, reported
status and outcome (resistant, sensitive or intermediate). In this research,
the susceptibility test data were grouped firstly by specimen type. Moreover,
for each sample type, the data were grouped by pairs (pathogen, antimicrobial)
since it is widely accepted by clinicians as detailed in the UK five year
strategy in AMR.
A small dataset will be used for this example.
28 # Libraries
29 import numpy as np
30 import pandas as pd
31 import seaborn as sns
32 import matplotlib as mpl
33 import matplotlib.pyplot as plt
34
35 # Import from pyAMR
36 from pyamr.datasets.load import make_susceptibility
37
38 try:
39 __file__
40 TERMINAL = True
41 except:
42 TERMINAL = False
43
44 # -------------------------------------------
45 # Load data
46 # -------------------------------------------
47 # Load data
48 data = make_susceptibility()
49 data = data.drop_duplicates()
50
51 # Show
52 print("\nData:")
53 print(data)
54 print("\nColumns:")
55 print(data.dtypes)
56 print("\nUnique:")
57 print(data[[
58 'microorganism_code',
59 'antimicrobial_code',
60 'specimen_code',
61 'laboratory_number',
62 'patient_id']].nunique())
Data:
date_received date_outcome patient_id laboratory_number specimen_code specimen_name specimen_description ... microorganism_name antimicrobial_code antimicrobial_name sensitivity_method sensitivity mic reported
0 2009-01-03 NaN 20091 X428501 BLDCUL NaN blood ... klebsiella AAMI amikacin NaN sensitive NaN NaN
1 2009-01-03 NaN 20091 X428501 BLDCUL NaN blood ... klebsiella AAMO amoxycillin NaN resistant NaN NaN
2 2009-01-03 NaN 20091 X428501 BLDCUL NaN blood ... klebsiella AAUG augmentin NaN sensitive NaN NaN
3 2009-01-03 NaN 20091 X428501 BLDCUL NaN blood ... klebsiella AAZT aztreonam NaN sensitive NaN NaN
4 2009-01-03 NaN 20091 X428501 BLDCUL NaN blood ... klebsiella ACAZ ceftazidime NaN sensitive NaN NaN
... ... ... ... ... ... ... ... ... ... ... ... ... ... .. ...
319117 2009-12-31 NaN 24645 H2012337 BLDCUL NaN blood ... enterococcus AAMO amoxycillin NaN sensitive NaN NaN
319118 2009-12-31 NaN 24645 H2012337 BLDCUL NaN blood ... enterococcus ALIN linezolid NaN sensitive NaN NaN
319119 2009-12-31 NaN 24645 H2012337 BLDCUL NaN blood ... enterococcus ASYN synercid NaN resistant NaN NaN
319120 2009-12-31 NaN 24645 H2012337 BLDCUL NaN blood ... enterococcus ATEI teicoplanin NaN sensitive NaN NaN
319121 2009-12-31 NaN 24645 H2012337 BLDCUL NaN blood ... enterococcus AVAN vancomycin NaN sensitive NaN NaN
[319122 rows x 15 columns]
Columns:
date_received object
date_outcome float64
patient_id int64
laboratory_number object
specimen_code object
specimen_name float64
specimen_description object
microorganism_code object
microorganism_name object
antimicrobial_code object
antimicrobial_name object
sensitivity_method float64
sensitivity object
mic float64
reported float64
dtype: object
Unique:
microorganism_code 67
antimicrobial_code 58
specimen_code 22
laboratory_number 34816
patient_id 24646
dtype: int64
Computing SARI
The Single Antimicrobial Resistance Index or SARI describes the proportion
of resistant isolates for a given set of susceptibility tests. It provides a
value within the range [0, 1] where values close to one indicate high resistance.
It is agnostic to pathogen, antibiotic and/or time. The variables R, I and
S represent the number of susceptibility tests with Resistant, Intermediate and
Susceptible outcomes respectively. The definition might vary slightly since the
intermediate category is not always considered.
For more information see: pyamr.core.sari.SARI
For more examples see:
87 # -------------------------------------------
88 # Compute SARI
89 # -------------------------------------------
90 # Libraries
91 from pyamr.core.sari import SARI
92
93 # Create sari instance
94 sari = SARI(groupby=['specimen_code',
95 'microorganism_name',
96 'antimicrobial_name',
97 'sensitivity'])
98
99 # Compute SARI overall
100 sari_overall = sari.compute(data,
101 return_frequencies=True)
102
103 # Show
104 print("SARI (overall):")
105 print(sari_overall)
106
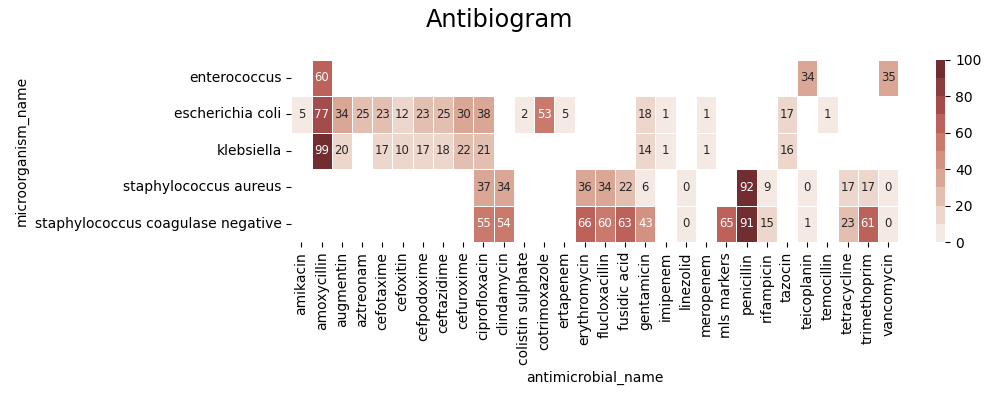
107 # ------------
108 # Plot Heatmap
109 # ------------
110 # Filter
111 matrix = sari_overall.copy(deep=True)
112 matrix = matrix.reset_index()
113 matrix = matrix[matrix.freq > 100]
114 matrix = matrix[matrix.specimen_code.isin(['BLDCUL'])]
115
116 # Pivot table
117 matrix = pd.pivot_table(matrix,
118 index='microorganism_name',
119 columns='antimicrobial_name',
120 values='sari')
121
122 # Create figure
123 f, ax = plt.subplots(1, 1, figsize=(10, 4))
124
125 # Create colormap
126 cmap = sns.color_palette("Reds", desat=0.5, n_colors=10)
127
128 # Plot
129 ax = sns.heatmap(data=matrix*100, annot=True, fmt=".0f",
130 annot_kws={'fontsize': 'small'}, cmap=cmap,
131 linewidth=0.5, vmin=0, vmax=100, ax=ax,
132 xticklabels=1, yticklabels=1)
133
134 # Add title
135 plt.suptitle("Antibiogram", fontsize='xx-large')
136
137 # Tight layout
138 plt.tight_layout()
139 plt.subplots_adjust(right=1.05)
SARI (overall):
intermediate resistant sensitive freq sari
specimen_code microorganism_name antimicrobial_name
BFLCUL anaerobes metronidazole 0.0 0.0 1.0 1.0 0.000000
bacillus ciprofloxacin 0.0 0.0 1.0 1.0 0.000000
clindamycin 0.0 3.0 1.0 4.0 0.750000
erythromycin 0.0 1.0 3.0 4.0 0.250000
fusidic acid 0.0 3.0 1.0 4.0 0.750000
... ... ... ... ... ...
XINCUL streptococcus beta-haemolytic group b cephalexin 0.0 1.0 0.0 1.0 1.000000
clindamycin 0.0 1.0 8.0 9.0 0.111111
erythromycin 0.0 1.0 8.0 9.0 0.111111
penicillin 0.0 0.0 9.0 9.0 0.000000
tetracycline 0.0 8.0 1.0 9.0 0.888889
[4491 rows x 5 columns]
Computing MARI
Warning
Pending… similar to SARI.
Computing ASAI
The antimicrobial spectrum of activity refers to the range of microbe species that are susceptible to these agents and therefore can be treated. In general, antimicrobial agents are classified into broad, intermediate or narrow spectrum. Broad spectrum antimicrobials are active against both Gram-positive and Gram-negative bacteria. In contrast, narrow spectrum antimicrobials have limited activity and are effective only against particular species of bacteria. While these profiles appeared in the mid-1950s, little effort has been made to define them. Furthermore, such ambiguous labels are overused for different and even contradictory purposes.
In order to compute the antimicrobial spectrum of activity index or ASAI, it
is necessary to previously obtain the overall resistance (SARI) for all the
microbe-antimicrobial pairs. Furthermore, by following the criteria used in the
narrow-broad approach, these pairs were grouped into Gram-positive and Gram-negative.
Briefly, the weighted proportion of species to which the antimicrobial
is effective is computed for each genus. These are later added up and normalized by
the number of genera tested. An antimicrobial is considered effective to treat a
particular species when the corresponding resistance index (SARI) is lower than
a given threshold.
For more information see: pyamr.core.asai.ASAI
For more examples see:
In order to compute ASAI, we need to have the following columns present
in our dataset: antimicrobial, microorganism_genus, microorganism_species
and resistance. Moreover, in this example we will compute the ASAI for each
gram_stain category independently so we will need the microorganism gram stain
information too. This information is available in the registries:
pyamr.datasets.registries
Lets include all this information using the MicroorganismRegistry.
191 # ------------------------------
192 # Include gram stain
193 # ------------------------------
194 # Libraries
195 from pyamr.datasets.registries import MicroorganismRegistry
196
197 # Load registry
198 mreg = MicroorganismRegistry()
199
200 # Format sari dataframe
201 dataframe = sari_overall.copy(deep=True)
202 dataframe = dataframe.reset_index()
203
204 # Create genus and species
205 dataframe[['genus', 'species']] = \
206 dataframe.microorganism_name \
207 .str.capitalize() \
208 .str.split(expand=True, n=1)
209
210 # Combine with registry information
211 dataframe = mreg.combine(dataframe, on='microorganism_name')
212
213 # Fill missing gram stain
214 dataframe.gram_stain = dataframe.gram_stain.fillna('u')
Now that we have the genus, species and gram_stain information,
lets compute ASAI.
222 # -------------------------------------------
223 # Compute ASAI
224 # -------------------------------------------
225 # Import specific libraries
226 from pyamr.core.asai import ASAI
227
228 # Create asai instance
229 asai = ASAI(column_genus='genus',
230 column_specie='species',
231 column_resistance='sari',
232 column_frequency='freq')
233
234 # Compute
235 scores = asai.compute(dataframe,
236 groupby=['specimen_code',
237 'antimicrobial_name',
238 'gram_stain'],
239 weights='uniform',
240 threshold=0.5,
241 min_freq=0)
242
243 # Stack
244 scores = scores.unstack()
245
246 # Filter and drop index.
247 scores = scores.filter(like='URICUL', axis=0)
248 scores.index = scores.index.droplevel()
249
250 # Show
251 print("\nASAI (overall):")
252 print(scores)
c:\users\kelda\desktop\repositories\github\pyamr\main\pyamr\core\asai.py:572: UserWarning:
Extreme resistances [0, 1] were found in the DataFrame. These
rows should be reviewed since these resistances might correspond
to pairs with low number of records.
c:\users\kelda\desktop\repositories\github\pyamr\main\pyamr\core\asai.py:583: UserWarning:
There are NULL values in columns that are required. These
rows will be ignored to safely compute ASAI. Please review
the DataFrame and address this inconsistencies. See below
for more information:
specimen_code 0
antimicrobial_name 0
gram_stain 0
GENUS 0
SPECIE 2414
RESISTANCE 0
ASAI (overall):
N_GENUS N_SPECIE ASAI_SCORE
gram_stain n p u n p u n p u
antimicrobial_name
amikacin 5.0 NaN NaN 5.0 NaN NaN 0.800000 NaN NaN
amoxycillin 2.0 2.0 NaN 2.0 7.0 NaN 0.500000 0.833333 NaN
amp c markers 4.0 NaN NaN 4.0 NaN NaN 0.250000 NaN NaN
augmentin 5.0 2.0 NaN 5.0 7.0 NaN 0.200000 1.000000 NaN
aztreonam 3.0 NaN NaN 3.0 NaN NaN 0.666667 NaN NaN
cefotaxime 5.0 NaN NaN 5.0 NaN NaN 0.200000 NaN NaN
cefoxitin 5.0 NaN NaN 5.0 NaN NaN 0.400000 NaN NaN
cefpodoxime 5.0 2.0 NaN 5.0 5.0 NaN 0.400000 0.833333 NaN
ceftazidime 5.0 NaN NaN 5.0 NaN NaN 0.600000 NaN NaN
cefuroxime 5.0 NaN NaN 5.0 NaN NaN 0.000000 NaN NaN
cephalexin 5.0 2.0 NaN 5.0 7.0 NaN 0.200000 0.875000 NaN
ciprofloxacin 6.0 2.0 NaN 6.0 7.0 NaN 0.333333 0.875000 NaN
clindamycin NaN 2.0 NaN NaN 4.0 NaN NaN 1.000000 NaN
colistin sulphate 5.0 NaN NaN 5.0 NaN NaN 0.800000 NaN NaN
cotrimoxazole 3.0 NaN NaN 3.0 NaN NaN 0.333333 NaN NaN
ertapenem 3.0 NaN NaN 3.0 NaN NaN 0.666667 NaN NaN
erythromycin NaN 2.0 NaN NaN 6.0 NaN NaN 0.833333 NaN
esbl markers 5.0 NaN NaN 5.0 NaN NaN 0.200000 NaN NaN
flucloxacillin 1.0 1.0 NaN 1.0 3.0 NaN 0.000000 1.000000 NaN
fusidic acid NaN 1.0 NaN NaN 3.0 NaN NaN 0.666667 NaN
gentamicin 5.0 1.0 NaN 5.0 3.0 NaN 0.800000 1.000000 NaN
imipenem 5.0 NaN NaN 5.0 NaN NaN 0.600000 NaN NaN
linezolid NaN 1.0 NaN NaN 3.0 NaN NaN 1.000000 NaN
mecillinam 5.0 NaN NaN 5.0 NaN NaN 0.400000 NaN NaN
meropenem 5.0 NaN NaN 5.0 NaN NaN 0.600000 NaN NaN
mls markers NaN 1.0 NaN NaN 3.0 NaN NaN 0.333333 NaN
mupirocin NaN 1.0 NaN NaN 2.0 NaN NaN 1.000000 NaN
naladixic acid 1.0 NaN NaN 1.0 NaN NaN 1.000000 NaN NaN
nitrofurantoin 5.0 2.0 NaN 5.0 7.0 NaN 0.200000 1.000000 NaN
novobiocin 1.0 1.0 NaN 1.0 3.0 NaN 0.000000 0.666667 NaN
penicillin 1.0 2.0 NaN 1.0 6.0 NaN 0.000000 0.500000 NaN
rifampicin NaN 1.0 NaN NaN 3.0 NaN NaN 1.000000 NaN
sulphamethoxazole 2.0 NaN NaN 2.0 NaN NaN 0.500000 NaN NaN
tazocin 5.0 NaN NaN 5.0 NaN NaN 0.800000 NaN NaN
teicoplanin NaN 2.0 NaN NaN 7.0 NaN NaN 1.000000 NaN
temocillin 3.0 NaN NaN 3.0 NaN NaN 0.666667 NaN NaN
tetracycline 1.0 2.0 NaN 1.0 6.0 NaN 1.000000 0.833333 NaN
timentin 4.0 NaN NaN 4.0 NaN NaN 0.750000 NaN NaN
tobramycin 5.0 NaN NaN 5.0 NaN NaN 0.600000 NaN NaN
trimethoprim 5.0 2.0 NaN 5.0 7.0 NaN 0.200000 1.000000 NaN
vancomycin NaN 2.0 NaN NaN 7.0 NaN NaN 1.000000 NaN
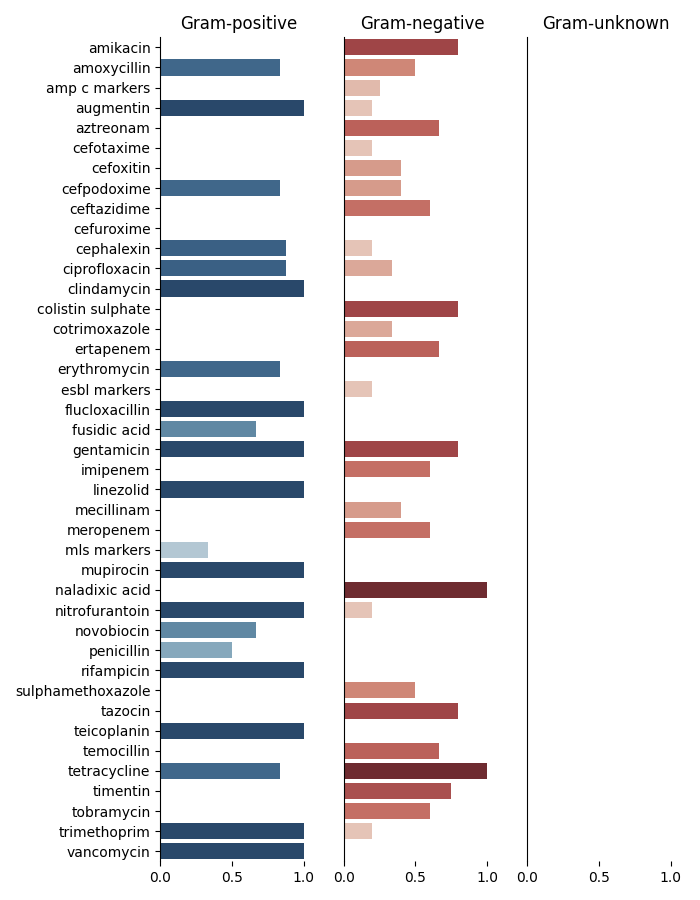
This is the information obtained where the columns n, p, and u stand for gram-positive, gram-negative and unknown respectively. Similarly, N_GENUS and N_SPECIE indicates the number of genus and species for the specific antimicrobial.
259 scores.head(10)
Lets plot it now!
265 # ---------------------------------------------------------------
266 # Plot
267 # ---------------------------------------------------------------
268 # .. note: In order to sort the scores we need to compute metrics
269 # that combine the different subcategories (e.g. gram-negative
270 # and gram-positive). Two possible options are: (i) use the
271 # gmean or (ii) the width.
272
273 # Libraries
274 from pyamr.utils.plot import scalar_colormap
275
276 # Measures
277 scores['width'] = np.abs(scores['ASAI_SCORE'].sum(axis=1))
278
279 # Variables to plot.
280 x = scores.index.values
281 y_n = scores['ASAI_SCORE']['n'].values
282 y_p = scores['ASAI_SCORE']['p'].values
283 y_u = scores['ASAI_SCORE']['u'].values
284
285 # Constants
286 colormap_p = scalar_colormap(y_p, cmap='Blues', vmin=-0.1, vmax=1.1)
287 colormap_n = scalar_colormap(y_n, cmap='Reds', vmin=-0.1, vmax=1.1)
288 colormap_u = scalar_colormap(y_u, cmap='Greens', vmin=-0.1, vmax=1.1)
289
290 # ----------
291 # Example
292 # ----------
293 # This example shows an stacked figure using more than two categories.
294 # For instance, it uses gram-positive, gram-negative and gram-unknown.
295 # All the indexes go within the range [0,1].
296 # Create the figure
297 f, axes = plt.subplots(1, 3, figsize=(7, 9))
298
299 # Plot each category
300 sns.barplot(x=y_p, y=x, palette=colormap_p, ax=axes[0], orient='h',
301 saturation=0.5, label='Gram-positive')
302 sns.barplot(x=y_n, y=x, palette=colormap_n, ax=axes[1], orient='h',
303 saturation=0.5, label='Gram-negative')
304 sns.barplot(x=y_u, y=x, palette=colormap_u, ax=axes[2], orient='h',
305 saturation=0.5, label='Gram-unknown')
306
307 # Configure
308 sns.despine(bottom=True)
309
310 # Format figure
311 plt.subplots_adjust(wspace=0.0, hspace=0.0)
312
313 # Remove yticks
314 axes[1].set_yticks([])
315 axes[2].set_yticks([])
316
317 # Set title
318 axes[0].set_title('Gram-positive')
319 axes[1].set_title('Gram-negative')
320 axes[2].set_title('Gram-unknown')
321
322 # Set x-axis
323 axes[0].set_xlim([0, 1.1])
324 axes[1].set_xlim([0, 1.1])
325 axes[2].set_xlim([0, 1.1])
326
327 # Adjust
328 plt.tight_layout()
Computing SART
The single antimicrobial resistance trend or SART measures the ratio
of change per time unit (e.g. monthly or yearly). To compute this metric,
it is necessary to generate a resistance time series from the susceptibility
test data. This is often achieved by computing the SARI on consecutive or
overlapping partitions of the data. Then, the trend can be extracted using
for example a linear model where the slope, which is represented by a value
within the range [-1, 1], indicates the ratio of change.
For more information see: pyamr.core.sart.SART
For more examples see:
Note
Be cautious when computing the SART index using a small dataset
(e.g. a low number of susceptibility tests records) since it is very
likely that the statistics produced (e.g. kurtosis or skewness) will
be ill defined. Also remember to check stationarity if using ARIMA.
Since it is necessary to have a decent amount of records to be able to compute the trends accurately, lets see which tuples have more number of samples.
361 # -------------------------------------------
362 # Show top combinations
363 # -------------------------------------------
364 from pyamr.core.sari import SARI
365
366 # Create SARI instance
367 sar = SARI(groupby=['specimen_code',
368 'microorganism_code',
369 'antimicrobial_code',
370 'sensitivity'])
371
372 # Compute SARI overall
373 sari_overall = sar.compute(data,
374 return_frequencies=True)
375
376 # Compute top tuples
377 top = sari_overall \
378 .sort_values(by='freq', ascending=False) \
379 .head(10)
380
381 # Show
382 print("\nTop by Frequency:")
383 print(top)
Top by Frequency:
intermediate resistant sensitive freq sari
specimen_code microorganism_code antimicrobial_code
URICUL ECOL A_CEFPODOX 0.0 595.0 8582.0 9177.0 0.064836
ANIT 0.0 347.0 8826.0 9173.0 0.037828
ACELX 0.0 803.0 8370.0 9173.0 0.087540
ATRI 0.0 3231.0 5941.0 9172.0 0.352268
ACIP 0.0 1259.0 7913.0 9172.0 0.137266
AAUG 0.0 602.0 8561.0 9163.0 0.065699
WOUCUL SAUR AFUS 0.0 613.0 3631.0 4244.0 0.144439
APEN 0.0 3677.0 566.0 4243.0 0.866604
AERY 0.0 1186.0 3056.0 4242.0 0.279585
AMET 0.0 869.0 3372.0 4241.0 0.204905
Let’s choose the tuples were are interested in.
388 # -------------------------------------------
389 # Filter data
390 # -------------------------------------------
391 # Define spec, orgs, abxs of interest
392 spec = ['URICUL']
393 orgs = ['ECOL']
394 abxs = ['ACELX', 'ACIP', 'AAMPC', 'ATRI', 'AAUG',
395 'AMER', 'ANIT', 'AAMI', 'ACTX', 'ATAZ',
396 'AGEN', 'AERT', 'ACAZ', 'AMEC', 'ACXT']
397
398 # Create auxiliary DataFrame
399 aux = data.copy(deep=True) \
400
401 # Filter
402 idxs_spec = data.specimen_code.isin(spec)
403 idxs_orgs = data.microorganism_code.isin(orgs)
404 idxs_abxs = data.antimicrobial_code.isin(abxs)
405
406 # Filter
407 aux = aux[idxs_spec & idxs_orgs & idxs_abxs]
Now, lets compute the resistance trend.
414 # Libraries
415 import warnings
416
417 # Import specific libraries
418 from pyamr.core.sart import SART
419
420 # Variables
421 shift, period = '10D', '180D'
422
423 # Create instance
424 sar = SART(column_specimen='specimen_code',
425 column_microorganism='microorganism_code',
426 column_antimicrobial='antimicrobial_code',
427 column_date='date_received',
428 column_outcome='sensitivity',
429 column_resistance='sari')
430
431 with warnings.catch_warnings():
432 warnings.simplefilter('ignore')
433
434 # Compute resistance trends
435 table, objs = sar.compute(aux, shift=shift,
436 period=period, return_objects=True)
1/15. Computing... ('URICUL', 'ECOL', 'AAMI')
2/15. Computing... ('URICUL', 'ECOL', 'AAMPC')
3/15. Computing... ('URICUL', 'ECOL', 'AAUG')
4/15. Computing... ('URICUL', 'ECOL', 'ACAZ')
5/15. Computing... ('URICUL', 'ECOL', 'ACELX')
6/15. Computing... ('URICUL', 'ECOL', 'ACIP')
7/15. Computing... ('URICUL', 'ECOL', 'ACTX')
8/15. Computing... ('URICUL', 'ECOL', 'ACXT')
9/15. Computing... ('URICUL', 'ECOL', 'AERT')
10/15. Computing... ('URICUL', 'ECOL', 'AGEN')
11/15. Computing... ('URICUL', 'ECOL', 'AMEC')
12/15. Computing... ('URICUL', 'ECOL', 'AMER')
13/15. Computing... ('URICUL', 'ECOL', 'ANIT')
14/15. Computing... ('URICUL', 'ECOL', 'ATAZ')
15/15. Computing... ('URICUL', 'ECOL', 'ATRI')
Lets see the results(note it is transposed!)
442 # Configure pandas
443 pd.set_option(
444 'display.max_colwidth', 20,
445 'display.width', 1000
446 )
447
448 # Show
449 #print("Results:")
450 #print(table.T)
451 table.head(4).T
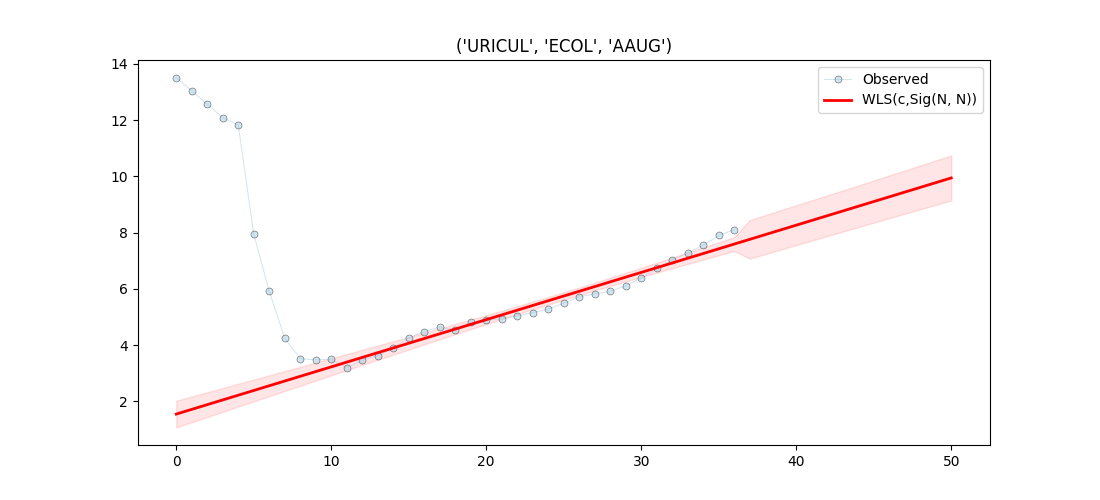
Lets visualise the first entry
457 # Display
458 # This example shows how to make predictions using the wrapper and how
459 # to plot the result in data. In addition, it compares the intervals
460 # provided by get_prediction (confidence intervals) and the intervals
461 # provided by wls_prediction_std (prediction intervals).
462
463 # Variables
464 name, obj = objs[2] # AAUG
465
466 # Series
467 series = obj.as_series()
468
469 # Variables.
470 start, end = None, 50
471
472 # Get x and y
473 x = series['wls-exog'][:,1]
474 y = series['wls-endog']
475
476 # Compute predictions (exogenous?). It returns a 2D array
477 # where the rows contain the time (t), the mean, the lower
478 # and upper confidence (or prediction?) interval.
479 preds = obj.get_prediction(start=start, end=end)
480
481 # Create figure
482 fig, ax = plt.subplots(1, 1, figsize=(11, 5))
483
484 # Plotting confidence intervals
485 # -----------------------------
486 # Plot truth values.
487 ax.plot(x, y, color='#A6CEE3', alpha=0.5, marker='o',
488 markeredgecolor='k', markeredgewidth=0.5,
489 markersize=5, linewidth=0.75, label='Observed')
490
491 # Plot forecasted values.
492 ax.plot(preds[0, :], preds[1, :], color='#FF0000', alpha=1.00,
493 linewidth=2.0, label=obj._identifier(short=True))
494
495 # Plot the confidence intervals.
496 ax.fill_between(preds[0, :], preds[2, :],
497 preds[3, :],
498 color='r',
499 alpha=0.1)
500
501 # Legend
502 plt.legend()
503 plt.title(name)
Text(0.5, 1.0, "('URICUL', 'ECOL', 'AAUG')")
Lets see the summary
508 # Summary
509 print("Name: %s\n" % str(name))
510 print(obj.as_summary())
Name: ('URICUL', 'ECOL', 'AAUG')
WLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.906
Model: WLS Adj. R-squared: 0.904
Method: Least Squares F-statistic: 339.1
Date: Thu, 15 Jun 2023 Prob (F-statistic): 1.38e-19
Time: 18:15:41 Log-Likelihood: -inf
No. Observations: 37 AIC: inf
Df Residuals: 35 BIC: inf
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 1.5450 0.235 6.578 0.000 1.068 2.022
x1 0.1679 0.009 18.416 0.000 0.149 0.186
==============================================================================
Omnibus: 5.037 Durbin-Watson: 0.176
Prob(Omnibus): 0.081 Jarque-Bera (JB): 2.336
Skew: 0.316 Prob(JB): 0.311
Kurtosis: 1.944 Cond. No. 91.7
Normal (N): 21.394 Prob(N): 0.000
==============================================================================
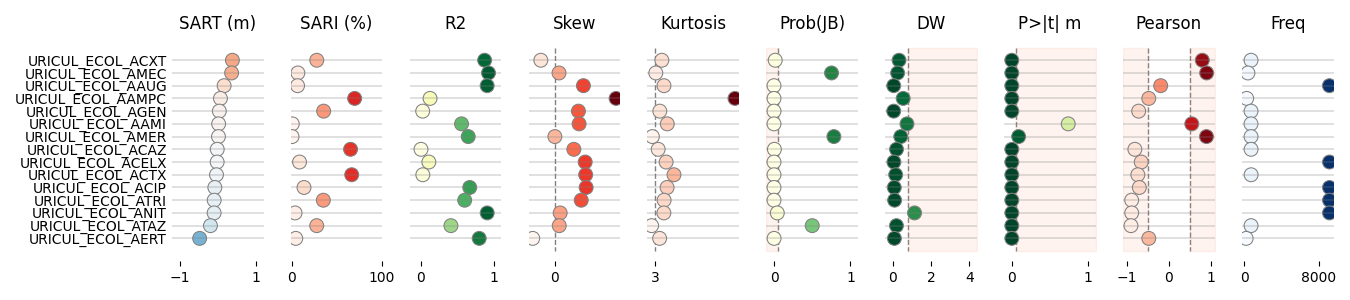
Lets display the information as a table graph for all tuples
516 # Libraries
517 from pyamr.graphics.table_graph import _DEFAULT_CONFIGURATION
518 from pyamr.graphics.table_graph import vlinebgplot
519
520 # Configuration for display
521 info = _DEFAULT_CONFIGURATION
522
523 # Lets define one as an example.
524 info['freq'] = {
525 'cmap': 'Blues',
526 'title': 'Freq',
527 'xticks': [0, 8000],
528 'kwargs': {
529 's': 80,
530 'vmin': 0
531 }
532 }
533
534 # .. note: It is important to ensure that the column names
535 # match with the keys of the previously loaded
536 # info configuration so that it is used.
537
538 # Rename columns
539 rename = {
540 'wls-x1_coef': 'sart_m',
541 'wls-const_coef': 'offset',
542 'wls-rsquared': 'r2',
543 'wls-rsquared_adj': 'r2_adj',
544 'wls-m_skew': 'skew',
545 'wls-m_kurtosis': 'kurtosis',
546 'wls-m_jb_prob': 'jb',
547 'wls-m_dw': 'dw',
548 'wls-const_tprob': 'ptm',
549 'wls-x1_tprob': 'ptn',
550 'wls-pearson': 'pearson',
551 'freq': 'freq',
552 }
553
554
555 # ----------------
556 # Combine with SARI
557
558 # Format combined DataFrame
559 comb = table.join(sari_overall)
560 comb.index = comb.index.map('_'.join)
561 comb = comb.reset_index()
562 comb = comb.rename(columns=rename)
563
564 # Add new columns
565 comb['sart_y'] = comb.sart_m * 12 # Yearly trend
566 comb['sari_pct'] = comb.sari * 100 # SARI percent
567
568 # Sort by trend
569 comb = comb.sort_values(by='sart_y', ascending=False)
570
571 # Select only numeric columns
572 # data = comb.select_dtypes(include=np.number)
573 data = comb[[
574 'index',
575 'sart_m',
576 #'sart_y',
577 'sari_pct',
578 'r2',
579 #'r2_adj',
580 'skew',
581 'kurtosis',
582 'jb',
583 'dw',
584 'ptm',
585 #'ptn',
586 'pearson',
587 'freq'
588 ]]
589
590 # Show DataFrame
591 #print("\nResults:")
592 #print(data)
593
594 # Create pair grid
595 g = sns.PairGrid(data, x_vars=data.columns[1:],
596 y_vars=["index"], height=3, aspect=.45)
597
598 # Set common features
599 g.set(xlabel='', ylabel='')
600
601 # Plot strips and format axes (skipping index)
602 for ax, c in zip(g.axes.flat, data.columns[1:]):
603
604 # Get information
605 d = info[c] if c in info else {}
606
607 # .. note: We need to use scatter plot if we want to
608 # assign colors to the markers according to
609 # their value.
610
611 # Using scatter plot
612 sns.scatterplot(data=data, x=c, y='index', s=100,
613 ax=ax, linewidth=0.75, edgecolor='gray',
614 c=data[c], cmap=d.get('cmap', None),
615 norm=d.get('norm', None))
616
617 # Plot vertical lines
618 for e in d.get('vline', []):
619 vlinebgplot(ax, top=data.shape[0], **e)
620
621 # Configure axes
622 ax.set(title=d.get('title', c),
623 xlim=d.get('xlim', None),
624 xticks=d.get('xticks', []),
625 xlabel='', ylabel='')
626 ax.tick_params(axis='y', which='both', length=0)
627 ax.xaxis.grid(False)
628 ax.yaxis.grid(visible=True, which='major',
629 color='gray', linestyle='-', linewidth=0.35)
630
631 # Despine
632 sns.despine(left=True, bottom=True)
633
634 # Adjust layout
635 plt.tight_layout()
636 plt.show()
637
638 #%
639 # Lets see the data plotted
640 data.round(decimals=3)
Computing ACSI
Warning
Pending…
Computing DRI
Warning
Pending…
Total running time of the script: ( 0 minutes 6.004 seconds)