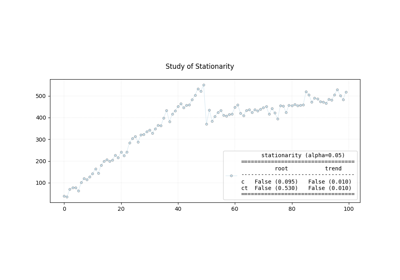
pyamr.core.stats.adfuller pyamr.core.stats.adfuller ========================= =========================

Classes

class pyamr.core.stats.adfuller.ADFWrapper(estimator=None, evaluate=True)[source]

The Augmented Dickey-Fuller test can be used to test for a unit root in a univariate process in the presence of serial correlation. It tests the null hypothesis that a unit root is present in a time series sample. The alternative hypothesis is different depending on which version of the test is used, but is usually stationarity or trend-stationarity. The more negative the statistic, the stronger the rejection of the hypothesis that there is a unit root at some level of confidence.

H	Hypothesis	Stationarity
H0	The series has a unit root	`Non-stationary`
H1	The series has no unit root	`Stationary` / `Trend-Stationary`

If p-value > 0.05: Failed to reject H0.

If p-value <= 0.05: Reject H0.

The absence of unit root is not a proof of non-stationarity. As such, it is also possible to use the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test to identify the existence of an underlying trend which can also be removed to obtain a stationary process. These are called trend-stationary processes.

In both, unit-root and trend-stationary processes, the mean can be increasing or decreasing over time; however, in the presence of a shock, trend-stationary processes revert to this mean tendency in the long run (deterministic trend) while unit-root processes have a permanent impact (stochastic trend).

Methods:

`as_summary`([alpha, verbose])	This method creates the summary to display.
`evaluate`(**kwargs)	Evaluates the model.
`is_stationary`([alpha])	This method returns a boolean with the stationarity outocme.
`stationarity`([alpha])	This method returns the stationarity outcome.