pyamr.core.stats.stationarity

Classes

class pyamr.core.stats.stationarity.StationarityWrapper(estimator=None, evaluate=True)

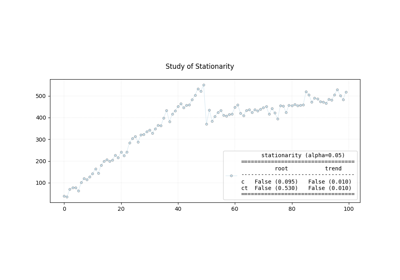
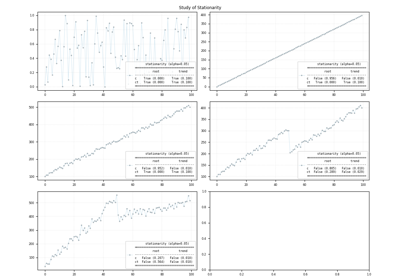
In time series analysis, “stationarity” refers to a key assumption about the behavior of a time series over time. A stationary time series is one in which statistical properties, such as mean, variance, and autocorrelation, remain constant over time. Stationarity is an important concept because many time series analysis techniques rely on this assumption for their validity. There are different types of stationarity that can be observed in time series data.

The augmented Dickey–Fuller test or ADF can be used to determine the presence of a unit root. When the other roots of the characteristic function lie inside the unit circle the first difference of the process is stationary. Due to this property, these are also called difference-stationary processes. Since the absence of unit root is not a proof of non-stationarity, the Kwiatkowski–Phillips–Schmidt–Shin or KPSS test can be used to identify the existence of an underlying trend which can also be removed to obtain a stationary process. These are called trend-stationary processes. In both, unit-root and trend-stationary processes, the mean can be increasing or decreasing over time; however, in the presence of a shock, trend-stationary processes (blue) revert to this mean tendency in the long run (deterministic trend) while unit-root processes (green) have a permanent impact (stochastic trend). The significance level of the tests is usually set to 0.05.

ADF	KPSS	Outcome	Note
Non-Stationary	Non-Stationary	Non-Stationary
Stationary	Stationary	Stationary
Non-Stationary	Stationary	Trend-Stationary	Check the de-trended series
Stationary	Non-Stationary	Difference-Stationary	Check the differenced series

Methods:

as_summary([alpha])	This method creates the summary to display.
evaluate([alpha])	This method initialises the series.
fit(x[, adf_kwargs, kpss_kwargs])	This method studies the stationarity of a given time-series.

as_summary(alpha=0.05)

This method creates the summary to display.

evaluate(alpha=0.05, **kwargs)

This method initialises the series.

fit(x, adf_kwargs={}, kpss_kwargs={}, **kwargs)

This method studies the stationarity of a given time-series.

The parameters which can be passed to the adfuller and kpss methods are listed below:

• adfuller_kwargs = {x, maxlag, regression, autolag, store, regresults}

• kpss_kwargs = {x, regression, lags, store}

@see statsmodels.tsa.stattools.adfuller @see statsmodels.tsa.stattoosl.kpss

Parameters:

• x (array-like) – The time series

• adf_kwargs (dict-like) – The parameters to pass to the adfuller function

• kpss_kwargs (dict-like) – The parameters to apss to the kpss function

Returns:

object

Return type:

An StationarityWrapper objects.

Examples using pyamr.core.stats.stationarity.StationarityWrapper

Step 03 - Time Series Analysis

Step 03 - Time Series Analysis

Stationarity

Stationarity