Step 03 - Time Series Analysis

In this tutorial example, we will delve into the fascinating field of time series analysis and explore how to compute and analyze time series data. Time series analysis involves studying data points collected over regular intervals of time, with the aim of understanding patterns, trends, and relationships that may exist within the data. By applying statistical techniques, we can uncover valuable insights and make predictions based on historical trends.

Throughout this example, we will explore various statistical metrics and tests to that are commonly used for time series analysis, empowering you to harness the power of time-dependent data and extract meaningful information from it. The special focus is stationarity, which is a common requirements for further application of time series analysis methods.

See below for a few resources.

• R1: Understanding KPSS test for stationarity.

• R2: Understanding autoregressions.

Create time series (TS)

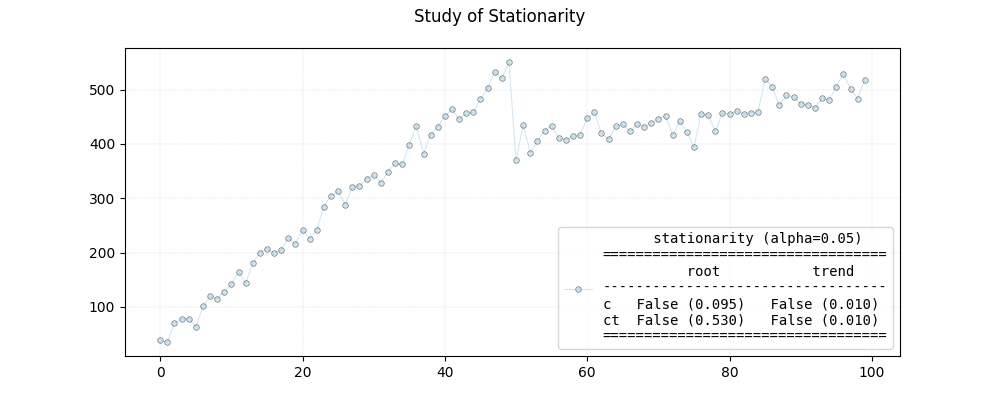
First lets create an artificial series. The series has been plotted ad the end of the tutorial.

# ----------------------------
# create data
# ----------------------------
# Import specific
from pyamr.datasets.load import make_timeseries

# Create timeseries data
x, y, f = make_timeseries()

Pearson correlation coefficient

It measures the linear correlation between two variables with a value within the range [-1,1]. Coefficient values of -1, 0 and 1 indicate total negative linear correlation, no linear correlation and total positive correlation respectively. In this study, the coefficient is used to assess whether or not there is a linear correlation between the number of observations (susceptibility test records) and the computed resistance index.

See also Correlation

# -------------------------------
# Pearson correlation coefficient
# -------------------------------
# Import pyAMR
from pyamr.core.stats.correlation import CorrelationWrapper

# Create object
correlation = CorrelationWrapper().fit(x1=y, x2=f)

# Print summary.
print("\n")
print(correlation.as_summary())

         Correlation
==============================
Pearson:                 0.784
Spearman:                0.790
Cross correlation: 5114836.774
==============================

Augmented Dickey-Fuller test

The Augmented Dickey-Fuller or ADF test can be used to test for a unit root in a univariate process in the presence of serial correlation. The intuition behind a unit root test is that it determines how strongly a time series is defined by a trend. ADF tests the null hypothesis that a unit root is present in a time series sample. The alternative hypothesis is different depending on which version of the test is used, but is usually stationarity or trend-stationarity. The more negative the statistic, the stronger the rejection of the hypothesis that there is a unit root at some level of confidence.

H	Hypothesis	Stationarity
H0	The series has a unit root	Non-stationary
H1	The series has no unit root	Stationary / Trend-Stationary

If p-value > 0.05: Failed to reject H0.

If p-value <= 0.05: Reject H0.

See also ADFuller

# ----------------------------
# ADFuller
# ----------------------------
# Import statsmodels
from statsmodels.tsa.stattools import adfuller

# Import pyAMR
from pyamr.core.stats.adfuller import ADFWrapper

# Create wrapper
adf = ADFWrapper(adfuller).fit(x=y, regression='ct')

print("\n")
print(adf.as_summary())

    adfuller test stationarity (ct)
=======================================
statistic:                       -2.128
pvalue:                         0.53020
nlags:                                1
nobs:                                98
stationarity (α=0.05):   non-stationary
=======================================

Kwiatkowski-Phillips-Schmidt-Shin test

The Kwiatkowski–Phillips–Schmidt–Shin or KPSS test is used to identify whether a time series is stationary around a deterministic trend (thus trend stationary) against the alternative of a unit root.

In the KPSS test, the absence of a unit root is not a proof of stationarity but, by design, of trend stationarity. This is an important distinction since it is possible for a time series to be non-stationary, have no unit root yet be trend-stationary.

In both, unit-root and trend-stationary processes, the mean can be increasing or decreasing over time; however, in the presence of a shock, trend-stationary processes revert to this mean tendency in the long run (deterministic trend) while unit-root processes have a permanent impact (stochastic trend).

H	Hypothesis	Stationarity
H0	The series has no unit root	Trend-stationary
H1	The series has a unit root	No Trend-Stationary

If p-value > alpha: Failed to reject H0

If p-value <= alpha: Reject H0

# --------------------------------
# Kpss
# --------------------------------
# Used within StationarityWrapper!

Understanding stationarity in TS

In time series analysis, “stationarity” refers to a key assumption about the behavior of a time series over time. A stationary time series is one in which statistical properties, such as mean, variance, and autocorrelation, remain constant over time. Stationarity is an important concept because many time series analysis techniques rely on this assumption for their validity. There are different types of stationarity that can be observed in time series data. Let’s explore them:

• Strict Stationarity: A time series is considered strictly stationary if the joint probability distribution of any set of its time points is invariant over time. This means that the statistical properties, such as mean, variance, and covariance, are constant across all time points.

• Weak Stationarity: Weak stationarity, also known as second-order stationarity or covariance stationarity, is a less strict form of stationarity. A time series is considered weakly stationary if its mean and variance are constant over time, and the autocovariance between any two time points only depends on the time lag between them. In other words, the statistical properties of the time series do not change with time.

• Trend Stationarity: Trend stationarity refers to a time series that exhibits a stable mean over time but may have a changing variance. This means that the data has a consistent trend component but the other statistical properties remain constant. In trend stationary series, the mean of the time series can be modeled by a constant or a linear trend.

• Difference Stationarity: Difference stationarity, also known as integrated stationarity, occurs when differencing a non-stationary time series results in a stationary series. Differencing involves computing the differences between consecutive observations to remove trends or other non-stationary patterns. A differenced time series is said to be difference stationary if it exhibits weak stationarity after differencing.

• Seasonal Stationarity: …

The augmented Dickey–Fuller test or ADF can be used to determine the presence of a unit root. When the other roots of the characteristic function lie inside the unit circle the first difference of the process is stationary. Due to this property, these are also called difference-stationary processes. Since the absence of unit root is not a proof of non-stationarity, the Kwiatkowski–Phillips–Schmidt–Shin or KPSS test can be used to identify the existence of an underlying trend which can also be removed to obtain a stationary process. These are called trend-stationary processes. In both, unit-root and trend-stationary processes, the mean can be increasing or decreasing over time; however, in the presence of a shock, trend-stationary processes (blue) revert to this mean tendency in the long run (deterministic trend) while unit-root processes (green) have a permanent impact (stochastic trend). The significance level of the tests is usually set to 0.05.

ADF	KPSS	Outcome	Note
Non-Stationary	Non-Stationary	Non-Stationary
Stationary	Stationary	Stationary
Non-Stationary	Stationary	Trend-Stationary	Check the de-trended series
Stationary	Non-Stationary	Difference-Stationary	Check the differenced-series

See also Stationarity

# ----------------------------
# Stationarity
# ----------------------------
# Import generic
import matplotlib.pyplot as plt

# Import pyAMR
from pyamr.core.stats.stationarity import StationarityWrapper

# Define kwargs
adf_kwargs = {}
kpss_kwargs = {}

# Compute stationarity
stationarity = StationarityWrapper().fit(x=y,
    adf_kwargs=adf_kwargs, kpss_kwargs=kpss_kwargs)

# Print summary.
print("\n")
print(stationarity.as_summary())


# ----------------
# plot
# ----------------
# Font type.
font = {
    'family': 'monospace',
    'weight': 'normal',
    'size': 10,
}

# Create figure
fig, ax = plt.subplots(1, 1, figsize=(10, 4))

# Plot truth values.
ax.plot(y, color='#A6CEE3', alpha=0.5, marker='o',
         markeredgecolor='k', markeredgewidth=0.5,
         markersize=4, linewidth=0.75,
         label=stationarity.as_summary())

# Format axes
ax.grid(color='gray', linestyle='--', linewidth=0.2, alpha=0.5)
ax.legend(prop=font, loc=4)

# Addd title
plt.suptitle("Study of Stationarity")

plt.show()

c:\users\kelda\desktop\repositories\github\pyamr\main\pyamr\core\stats\stationarity.py:187: InterpolationWarning:

The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is smaller than the p-value returned.


c:\users\kelda\desktop\repositories\github\pyamr\main\pyamr\core\stats\stationarity.py:188: InterpolationWarning:

The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is smaller than the p-value returned.


c:\users\kelda\desktop\repositories\github\pyamr\main\pyamr\core\stats\stationarity.py:189: InterpolationWarning:

The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is smaller than the p-value returned.


(3.2, 0.95, {'10%': 1.2888, '5%': 1.1412, '2.5%': 1.0243, '1%': 0.907})


      stationarity (alpha=0.05)
==================================
          root           trend
----------------------------------
c   False (0.095)   False (0.010)
ct  False (0.530)   False (0.010)
==================================