Note
Click here to download the full example code
05. Display SHAP for Sequential Data
This script provides an in-depth guide on visualizing SHAP values for sequential or time-series data, a common challenge when interpreting models like LSTMs or other RNNs. It explores various techniques to break down and display the complex, three-dimensional SHAP output (samples, timesteps, features).
The script demonstrates several approaches:
Slicing SHAP Data: It shows how to use the standard
shap.summary_plotby systematically slicing the data, visualizing feature importances either per-timestep or across all timesteps for a single feature.Custom Seaborn Plots: It implements custom visualizations using
seaborn.stripplotandseaborn.swarmplotto offer more granular control over the plot’s appearance and layout.Advanced Coloring: Helper functions are created to replicate SHAP’s signature feature—coloring data points by their original feature value—allowing for richer interpretation in custom plots.
This example is a valuable resource for anyone looking to move beyond default plots and create tailored, insightful SHAP visualizations for models that handle sequential data.
30 # Libraries
31 import shap
32 import numpy as np
33 import pandas as pd
34 import seaborn as sns
35
36 import matplotlib.pyplot as plt
37 import matplotlib as mpl
38 import matplotlib.colorbar
39 import matplotlib.colors
40 import matplotlib.cm
41
42 from mpl_toolkits.axes_grid1 import make_axes_locatable
43
44 try:
45 __file__
46 TERMINAL = True
47 except:
48 TERMINAL = False
49
50 # ------------------------
51 # Methods
52 # ------------------------
53 def scalar_colormap(values, cmap, vmin, vmax):
54 """This method creates a colormap based on values.
55
56 Parameters
57 ----------
58 values : array-like
59 The values to create the corresponding colors
60
61 cmap : str
62 The colormap
63
64 vmin, vmax : float
65 The minimum and maximum possible values
66
67 Returns
68 -------
69 scalar colormap
70 """
71 # Create scalar mappable
72 norm = mpl.colors.Normalize(vmin=vmin, vmax=vmax, clip=True)
73 mapper = mpl.cm.ScalarMappable(norm=norm, cmap=cmap)
74 # Get color map
75 colormap = sns.color_palette([mapper.to_rgba(i) for i in values])
76 # Return
77 return colormap, norm
78
79
80 def scalar_palette(values, cmap, vmin, vmax):
81 """This method creates a colorpalette based on values.
82
83 Parameters
84 ----------
85 values : array-like
86 The values to create the corresponding colors
87
88 cmap : str
89 The colormap
90
91 vmin, vmax : float
92 The minimum and maximum possible values
93
94 Returns
95 -------
96 scalar colormap
97
98 """
99 # Create a matplotlib colormap from name
100 #cmap = sns.light_palette(cmap, reverse=False, as_cmap=True)
101 cmap = sns.color_palette(cmap, as_cmap=True)
102 # Normalize to the range of possible values from df["c"]
103 norm = mpl.colors.Normalize(vmin=vmin, vmax=vmax)
104 # Create a color dictionary (value in c : color from colormap)
105 colors = {}
106 for cval in values:
107 colors.update({cval : cmap(norm(cval))})
108 # Return
109 return colors, norm
110
111
112 def create_random_shap(samples, timesteps, features):
113 """Create random LSTM data.
114
115 .. note: No need to create the 3D matrix and then reshape to
116 2D. It would be possible to create directly the 2D
117 matrix.
118
119 Parameters
120 ----------
121 samples: int
122 The number of observations
123 timesteps: int
124 The number of time steps
125 features: int
126 The number of features
127
128 Returns
129 -------
130 Stacked matrix with the data.
131
132 """
133 # .. note: Either perform a pre-processing step such as
134 # normalization or generate the features within
135 # the appropriate interval.
136 # Create dataset
137 x = np.random.randint(low=0, high=100,
138 size=(samples, timesteps, features))
139 y = np.random.randint(low=0, high=2, size=samples).astype(float)
140 i = np.vstack(np.dstack(np.indices((samples, timesteps))))
141
142 # Create DataFrame
143 df = pd.DataFrame(
144 data=np.hstack((i, x.reshape((-1, features)))),
145 columns=['sample', 'timestep'] + \
146 ['f%s'%j for j in range(features)]
147 )
148
149 df_stack = df.set_index(['sample', 'timestep']).stack()
150 df_stack = df_stack
151 df_stack.name = 'shap_values'
152 df_stack = df_stack.to_frame()
153 df_stack.index.names = ['sample', 'timestep', 'features']
154 df_stack = df_stack.reset_index()
155
156 df_stack['feature_values'] = np.random.randint(
157 low=0, high=100, size=df_stack.shape[0])
158
159 return df_stack
160
161
162 def load_shap_file():
163 data = pd.read_csv('./data/shap.csv')
164 data = data.iloc[: , 1:]
165 #data.timestep = data.timestep - (data.timestep.nunique() - 1)
166 return data
Lets generate and/or load the shap values.
171 # .. note: The right format to use for plotting depends
172 # on the library we use. The data structure is
173 # good when using seaborn
174 # Load data
175 data = create_random_shap(10, 6, 4)
176 #data = load_shap_file()
177 #data = data[data['sample'] < 100]
178
179 shap_values = pd.pivot_table(data,
180 values='shap_values',
181 index=['sample', 'timestep'],
182 columns=['features'])
183
184 feature_values = pd.pivot_table(data,
185 values='feature_values',
186 index=['sample', 'timestep'],
187 columns=['features'])
188
189 # Show
190 if TERMINAL:
191 print("\nShow:")
192 print(data)
193 print(shap_values)
194 print(feature_values)
Let’s see how data looks like
198 data.head(10)
Let’s see how shap_values looks like
202 shap_values.iloc[:10, :5]
Let’s see how feature_values looks like
206 feature_values.iloc[:10, :5]
Display using shap.summary_plot
The first option is to use the shap library to plot the results.
215 # Let's define/extract some useful variables.
216 N = 4 # max loops filter
217 TIMESTEPS = len(shap_values.index.unique(level='timestep')) # number of timesteps
218 SAMPLES = len(shap_values.index.unique(level='sample')) # number of samples
219
220 shap_min = data.shap_values.min()
221 shap_max = data.shap_values.max()
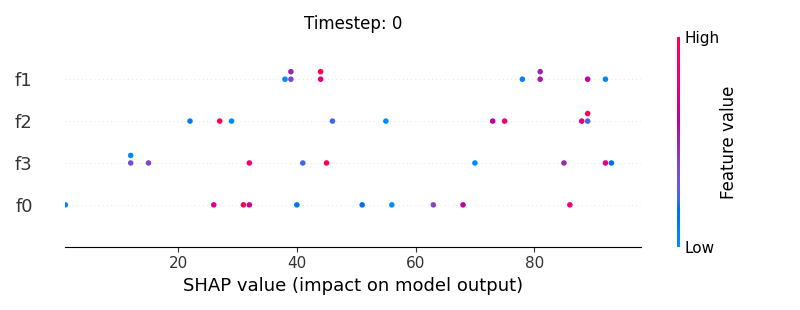
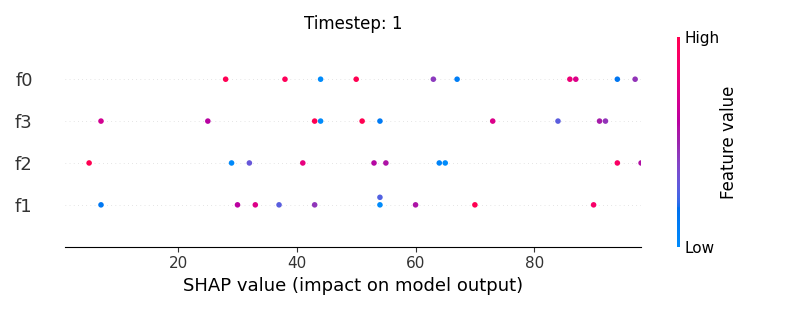
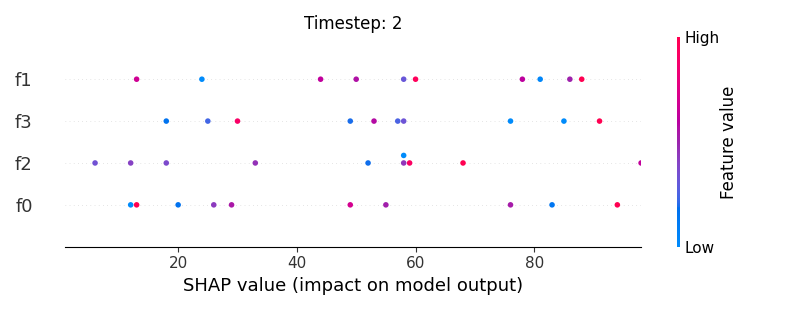
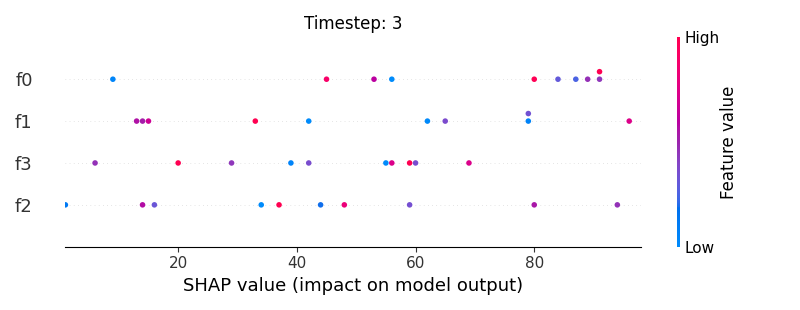
Now, let’s display the shap values for all features in each timestep.
226 # For each timestep (visualise all features)
227 for i, step in enumerate(range(TIMESTEPS)[:N]):
228 # Show
229 #print('%2d. %s' % (i, step))
230
231 # .. note: First option (commented) is only necessary if we work
232 # with a numpy array. However, since we are using a DataFrame
233 # with the timestep, we can index by that index level.
234 # Compute indices
235 #indice = np.arange(SAMPLES)*TIMESTEPS + step
236 indice = shap_values.index.get_level_values('timestep') == i
237
238 # Create auxiliary matrices
239 shap_aux = shap_values.iloc[indice]
240 feat_aux = feature_values.iloc[indice]
241
242 # Display
243 plt.figure()
244 plt.title("Timestep: %s" % i)
245 shap.summary_plot(shap_aux.to_numpy(), feat_aux, show=False)
246 plt.xlim(shap_min, shap_max)
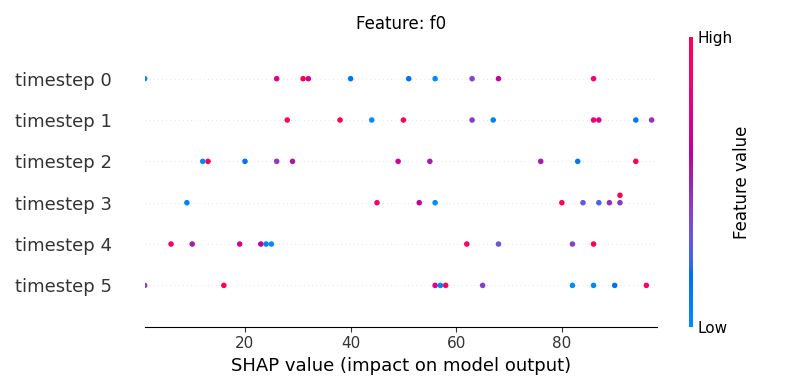
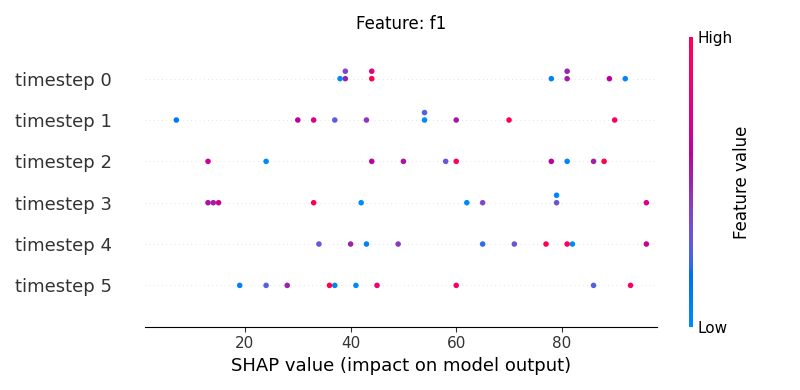
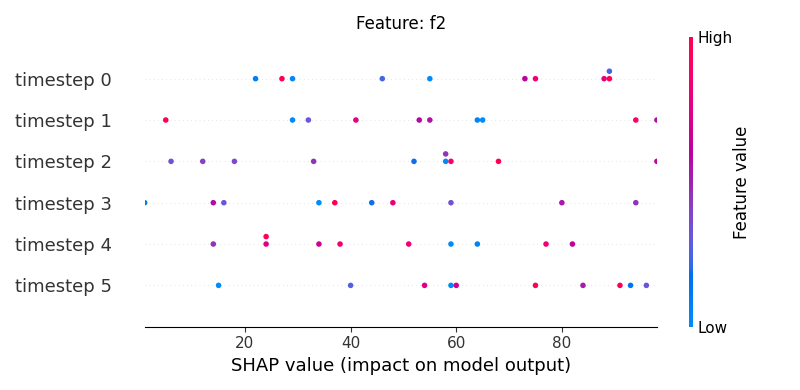
Now, let’s display the shap values for all timesteps of each feature.
251 # For each feature (visualise all time-steps)
252 for i, f in enumerate(shap_values.columns[:N]):
253 # Show
254 #print('%2d. %s' % (i, f))
255
256 # Create auxiliary matrices (select feature and reshape)
257 shap_aux = shap_values.iloc[:, i] \
258 .to_numpy().reshape(-1, TIMESTEPS)
259 feat_aux = feature_values.iloc[:, i] \
260 .to_numpy().reshape(-1, TIMESTEPS)
261 feat_aux = pd.DataFrame(feat_aux,
262 columns=['timestep %s'%j for j in range(TIMESTEPS)]
263 )
264
265 # Show
266 plt.figure()
267 plt.title("Feature: %s" % f)
268 shap.summary_plot(shap_aux, feat_aux, sort=False, show=False)
269 plt.xlim(shap_min, shap_max)
Note
If y-axis represents timesteps the sort parameter
in the summary_plot function is set to False.
Display using sns.stripplot
Warning
This method seems to be quite slow.
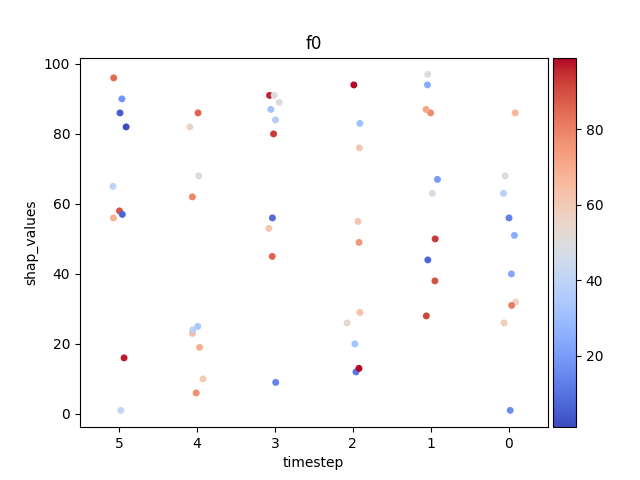
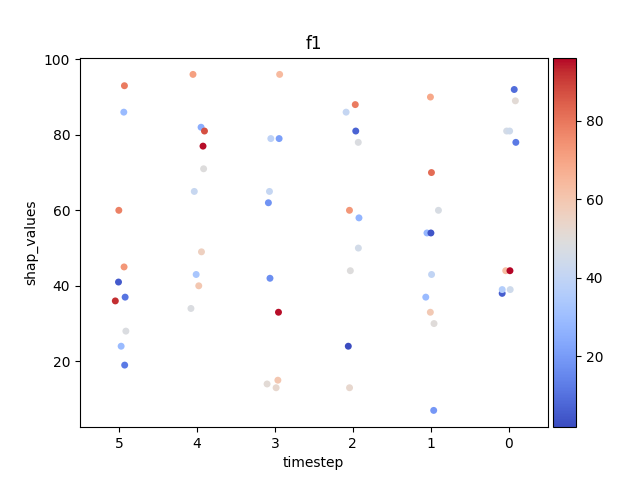
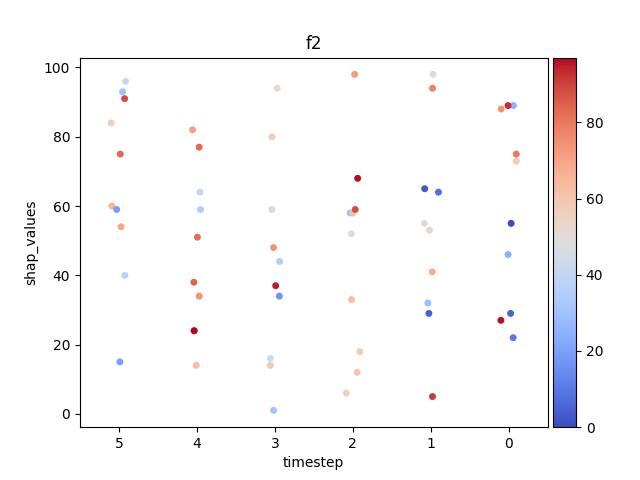
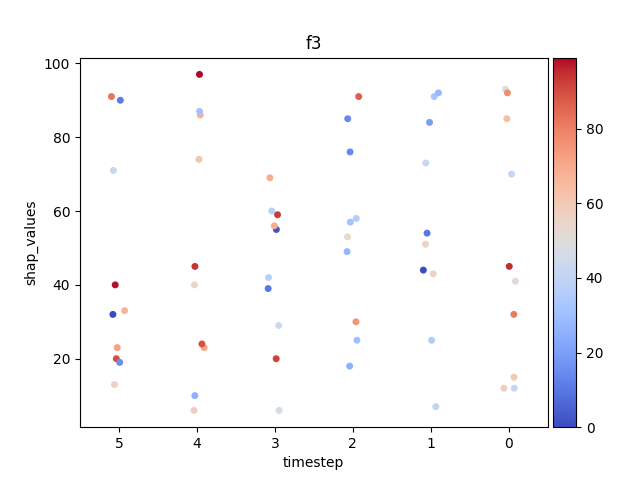
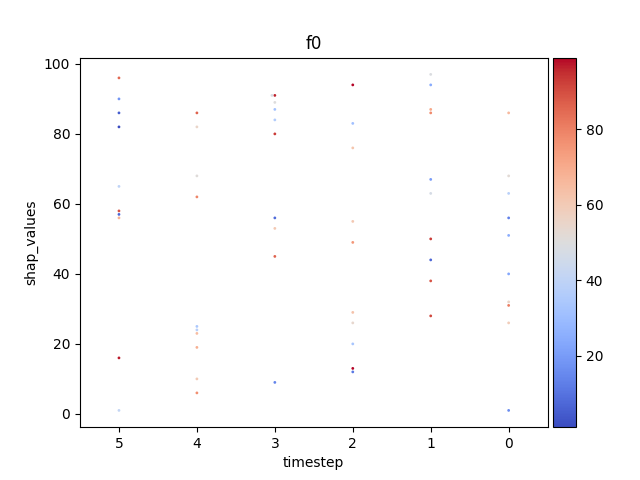
Let’s display the shap values for each feature and all time steps. In contrast to the previous example, the timesteps are now displayed on the x-axis and the y-axis contains the shap values.
286 def add_colorbar(fig, cmap, norm):
287 """"""
288 divider = make_axes_locatable(plt.gca())
289 ax_cb = divider.new_horizontal(size="5%", pad=0.05)
290 fig.add_axes(ax_cb)
291 cb1 = matplotlib.colorbar.ColorbarBase(ax_cb,
292 cmap=cmap, norm=norm, orientation='vertical')
293
294
295 # Loop
296 for i, (name, df) in enumerate(data.groupby('features')):
297
298 # Get colormap
299 values = df.feature_values
300 cmap, norm = scalar_palette(values=values, cmap='coolwarm',
301 vmin=values.min(), vmax=values.max())
302
303 print(df)
304
305 # Display
306 fig, ax = plt.subplots()
307 ax = sns.stripplot(x='timestep',
308 y='shap_values',
309 hue='feature_values',
310 palette=cmap,
311 data=df,
312 ax=ax)
313
314 # Needed for older matplotlib versions
315 cmap = matplotlib.cm.get_cmap('coolwarm')
316
317 # Configure axes
318 plt.title(name)
319 plt.legend([], [], frameon=False)
320 ax.invert_xaxis()
321 add_colorbar(plt.gcf(), cmap, norm)
322
323 # End
324 if int(i) > N:
325 break
326
327 # Show
328 plt.show()
Out:
sample timestep features shap_values feature_values
0 0 0 f0 61 65
4 0 1 f0 49 4
8 0 2 f0 68 0
12 0 3 f0 10 60
16 0 4 f0 11 61
20 0 5 f0 32 39
24 1 0 f0 53 36
28 1 1 f0 71 36
32 1 2 f0 74 6
36 1 3 f0 15 51
40 1 4 f0 56 13
44 1 5 f0 0 65
48 2 0 f0 24 66
52 2 1 f0 92 92
56 2 2 f0 50 15
60 2 3 f0 6 62
64 2 4 f0 43 45
68 2 5 f0 30 52
72 3 0 f0 28 36
76 3 1 f0 60 31
80 3 2 f0 26 64
84 3 3 f0 28 93
88 3 4 f0 82 29
92 3 5 f0 56 71
96 4 0 f0 37 68
100 4 1 f0 31 3
104 4 2 f0 57 95
108 4 3 f0 47 44
112 4 4 f0 89 52
116 4 5 f0 63 75
120 5 0 f0 30 86
124 5 1 f0 72 49
128 5 2 f0 20 40
132 5 3 f0 56 58
136 5 4 f0 64 26
140 5 5 f0 4 23
144 6 0 f0 20 85
148 6 1 f0 8 75
152 6 2 f0 50 93
156 6 3 f0 73 5
160 6 4 f0 98 98
164 6 5 f0 41 20
168 7 0 f0 45 80
172 7 1 f0 48 89
176 7 2 f0 31 51
180 7 3 f0 98 69
184 7 4 f0 3 5
188 7 5 f0 58 77
192 8 0 f0 26 18
196 8 1 f0 30 24
200 8 2 f0 92 72
204 8 3 f0 47 96
208 8 4 f0 9 45
212 8 5 f0 94 7
216 9 0 f0 64 86
220 9 1 f0 39 86
224 9 2 f0 27 13
228 9 3 f0 54 32
232 9 4 f0 4 54
236 9 5 f0 59 41
C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\shap\plot_main05.py:315: MatplotlibDeprecationWarning:
The get_cmap function was deprecated in Matplotlib 3.7 and will be removed in 3.11. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap()`` or ``pyplot.get_cmap()`` instead.
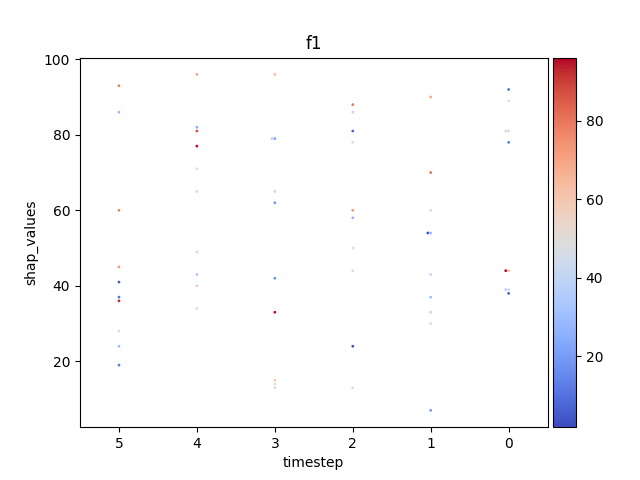
sample timestep features shap_values feature_values
1 0 0 f1 79 9
5 0 1 f1 66 71
9 0 2 f1 59 67
13 0 3 f1 7 85
17 0 4 f1 35 1
21 0 5 f1 62 94
25 1 0 f1 70 54
29 1 1 f1 31 40
33 1 2 f1 68 25
37 1 3 f1 99 6
41 1 4 f1 68 10
45 1 5 f1 66 4
49 2 0 f1 27 43
53 2 1 f1 64 69
57 2 2 f1 46 22
61 2 3 f1 92 38
65 2 4 f1 76 74
69 2 5 f1 92 11
73 3 0 f1 51 27
77 3 1 f1 99 52
81 3 2 f1 60 83
85 3 3 f1 34 65
89 3 4 f1 45 46
93 3 5 f1 86 88
97 4 0 f1 98 11
101 4 1 f1 2 46
105 4 2 f1 69 77
109 4 3 f1 14 55
113 4 4 f1 17 86
117 4 5 f1 90 0
121 5 0 f1 40 22
125 5 1 f1 65 93
129 5 2 f1 62 42
133 5 3 f1 67 50
137 5 4 f1 54 17
141 5 5 f1 45 69
145 6 0 f1 31 22
149 6 1 f1 44 45
153 6 2 f1 47 52
157 6 3 f1 1 8
161 6 4 f1 8 56
165 6 5 f1 27 79
169 7 0 f1 38 3
173 7 1 f1 53 7
177 7 2 f1 21 62
181 7 3 f1 34 62
185 7 4 f1 6 7
189 7 5 f1 12 41
193 8 0 f1 71 90
197 8 1 f1 81 82
201 8 2 f1 71 50
205 8 3 f1 41 12
209 8 4 f1 62 34
213 8 5 f1 96 93
217 9 0 f1 42 30
221 9 1 f1 35 52
225 9 2 f1 35 44
229 9 3 f1 51 56
233 9 4 f1 15 88
237 9 5 f1 4 19
C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\shap\plot_main05.py:315: MatplotlibDeprecationWarning:
The get_cmap function was deprecated in Matplotlib 3.7 and will be removed in 3.11. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap()`` or ``pyplot.get_cmap()`` instead.
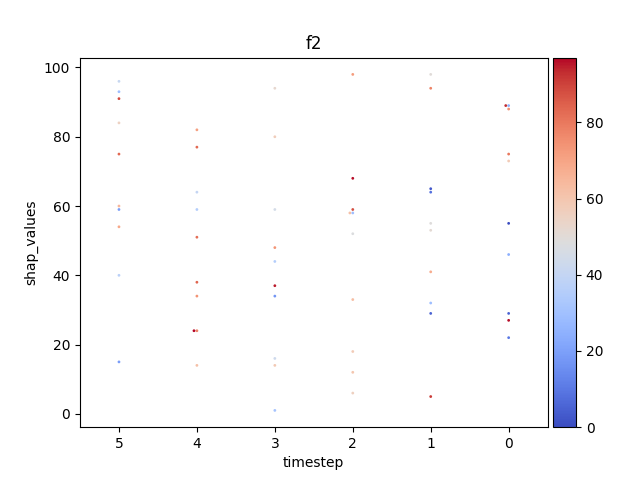
sample timestep features shap_values feature_values
2 0 0 f2 10 46
6 0 1 f2 24 86
10 0 2 f2 34 50
14 0 3 f2 13 49
18 0 4 f2 3 59
22 0 5 f2 90 19
26 1 0 f2 92 90
30 1 1 f2 45 52
34 1 2 f2 72 79
38 1 3 f2 65 13
42 1 4 f2 38 74
46 1 5 f2 24 97
50 2 0 f2 75 1
54 2 1 f2 40 38
58 2 2 f2 34 7
62 2 3 f2 34 73
66 2 4 f2 1 65
70 2 5 f2 41 9
74 3 0 f2 5 12
78 3 1 f2 10 48
82 3 2 f2 64 97
86 3 3 f2 14 5
90 3 4 f2 51 32
94 3 5 f2 83 95
98 4 0 f2 82 88
102 4 1 f2 85 55
106 4 2 f2 12 68
110 4 3 f2 5 0
114 4 4 f2 34 60
118 4 5 f2 95 23
122 5 0 f2 52 1
126 5 1 f2 0 12
130 5 2 f2 46 39
134 5 3 f2 74 36
138 5 4 f2 8 6
142 5 5 f2 67 1
146 6 0 f2 2 41
150 6 1 f2 17 34
154 6 2 f2 25 62
158 6 3 f2 23 70
162 6 4 f2 19 52
166 6 5 f2 74 7
170 7 0 f2 18 66
174 7 1 f2 81 66
178 7 2 f2 87 98
182 7 3 f2 24 10
186 7 4 f2 76 28
190 7 5 f2 54 7
194 8 0 f2 88 85
198 8 1 f2 47 1
202 8 2 f2 76 87
206 8 3 f2 73 98
210 8 4 f2 82 97
214 8 5 f2 11 98
218 9 0 f2 57 39
222 9 1 f2 96 20
226 9 2 f2 86 45
230 9 3 f2 61 42
234 9 4 f2 32 3
238 9 5 f2 91 2
C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\shap\plot_main05.py:315: MatplotlibDeprecationWarning:
The get_cmap function was deprecated in Matplotlib 3.7 and will be removed in 3.11. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap()`` or ``pyplot.get_cmap()`` instead.
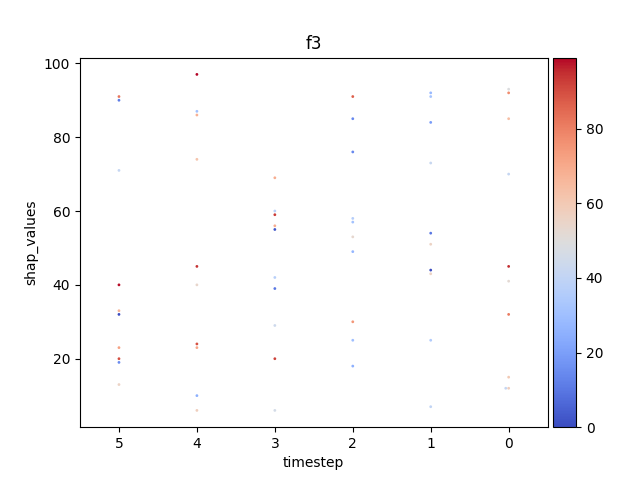
sample timestep features shap_values feature_values
3 0 0 f3 76 68
7 0 1 f3 38 32
11 0 2 f3 89 41
15 0 3 f3 68 82
19 0 4 f3 30 12
23 0 5 f3 89 8
27 1 0 f3 51 6
31 1 1 f3 27 74
35 1 2 f3 27 17
39 1 3 f3 82 70
43 1 4 f3 89 8
47 1 5 f3 42 74
51 2 0 f3 32 29
55 2 1 f3 87 64
59 2 2 f3 75 48
63 2 3 f3 99 94
67 2 4 f3 79 80
71 2 5 f3 51 66
75 3 0 f3 38 94
79 3 1 f3 54 56
83 3 2 f3 74 84
87 3 3 f3 46 22
91 3 4 f3 59 45
95 3 5 f3 59 82
99 4 0 f3 41 32
103 4 1 f3 76 46
107 4 2 f3 80 65
111 4 3 f3 87 61
115 4 4 f3 95 64
119 4 5 f3 49 46
123 5 0 f3 98 38
127 5 1 f3 55 50
131 5 2 f3 70 48
135 5 3 f3 74 47
139 5 4 f3 13 83
143 5 5 f3 59 52
147 6 0 f3 18 51
151 6 1 f3 9 5
155 6 2 f3 79 31
159 6 3 f3 67 48
163 6 4 f3 31 21
167 6 5 f3 43 44
171 7 0 f3 19 99
175 7 1 f3 77 10
179 7 2 f3 71 64
183 7 3 f3 80 37
187 7 4 f3 17 24
191 7 5 f3 30 95
195 8 0 f3 34 74
199 8 1 f3 45 6
203 8 2 f3 95 77
207 8 3 f3 84 30
211 8 4 f3 18 46
215 8 5 f3 40 90
219 9 0 f3 99 66
223 9 1 f3 29 23
227 9 2 f3 78 71
231 9 3 f3 95 59
235 9 4 f3 87 36
239 9 5 f3 27 4
C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\shap\plot_main05.py:315: MatplotlibDeprecationWarning:
The get_cmap function was deprecated in Matplotlib 3.7 and will be removed in 3.11. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap()`` or ``pyplot.get_cmap()`` instead.
C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\shap\plot_main05.py:328: UserWarning:
FigureCanvasAgg is non-interactive, and thus cannot be shown
Display using sns.swarmplot
Let’s display the shap values for each timestep.
342 # Loop
343 for i, (name, df) in enumerate(data.groupby('features')):
344
345 # Get colormap
346 values = df.feature_values
347 cmap, norm = scalar_palette(values=values, cmap='coolwarm',
348 vmin=values.min(), vmax=values.max())
349
350 # Display
351 fig, ax = plt.subplots()
352 ax = sns.swarmplot(x='timestep',
353 y='shap_values',
354 hue='feature_values',
355 palette=cmap,
356 data=df,
357 size=2,
358 ax=ax)
359
360 # Needed for older matplotlib versions
361 cmap = matplotlib.cm.get_cmap('coolwarm')
362
363 # Configure axes
364 plt.title(name)
365 plt.legend([], [], frameon=False)
366 ax.invert_xaxis()
367 add_colorbar(plt.gcf(), cmap, norm)
368
369 # End
370 if int(i) > N:
371 break
372
373 # Show
374 plt.show()
375
376
377
378
379
380
381
382 """
383 sns.set_theme(style="ticks")
384
385 # Create a dataset with many short random walks
386 rs = np.random.RandomState(4)
387 pos = rs.randint(-1, 2, (20, 5)).cumsum(axis=1)
388 pos -= pos[:, 0, np.newaxis]
389 step = np.tile(range(5), 20)
390 walk = np.repeat(range(20), 5)
391 df = pd.DataFrame(np.c_[pos.flat, step, walk],
392 columns=["position", "step", "walk"])
393 # Initialize a grid of plots with an Axes for each walk
394 #grid = sns.FacetGrid(df_stack, col="walk", hue="f", palette="tab20c",
395 # col_wrap=4, height=1.5)
396
397 grid = sns.FacetGrid(df_stack, hue="f",
398 palette="tab20c", height=1.5)
399
400 # Draw a horizontal line to show the starting point
401 grid.refline(y=0, linestyle=":")
402
403 # Draw a line plot to show the trajectory of each random walk
404 grid.map(plt.plot, "t", "value", marker="o")
405
406 # Adjust the tick positions and labels
407 grid.set(xticks=np.arange(5), yticks=[-3, 3],
408 xlim=(-.5, 4.5), ylim=(-3.5, 3.5))
409
410 # Adjust the arrangement of the plots
411 grid.fig.tight_layout(w_pad=1)
412
413 """
414
415
416 #plt.show()
Out:
C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\shap\plot_main05.py:361: MatplotlibDeprecationWarning:
The get_cmap function was deprecated in Matplotlib 3.7 and will be removed in 3.11. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap()`` or ``pyplot.get_cmap()`` instead.
C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\shap\plot_main05.py:361: MatplotlibDeprecationWarning:
The get_cmap function was deprecated in Matplotlib 3.7 and will be removed in 3.11. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap()`` or ``pyplot.get_cmap()`` instead.
C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\shap\plot_main05.py:361: MatplotlibDeprecationWarning:
The get_cmap function was deprecated in Matplotlib 3.7 and will be removed in 3.11. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap()`` or ``pyplot.get_cmap()`` instead.
C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\shap\plot_main05.py:361: MatplotlibDeprecationWarning:
The get_cmap function was deprecated in Matplotlib 3.7 and will be removed in 3.11. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap()`` or ``pyplot.get_cmap()`` instead.
C:\Users\kelda\Desktop\repositories\github\python-spare-code\main\examples\shap\plot_main05.py:374: UserWarning:
FigureCanvasAgg is non-interactive, and thus cannot be shown
'\nsns.set_theme(style="ticks")\n\n# Create a dataset with many short random walks\nrs = np.random.RandomState(4)\npos = rs.randint(-1, 2, (20, 5)).cumsum(axis=1)\npos -= pos[:, 0, np.newaxis]\nstep = np.tile(range(5), 20)\nwalk = np.repeat(range(20), 5)\ndf = pd.DataFrame(np.c_[pos.flat, step, walk],\n columns=["position", "step", "walk"])\n# Initialize a grid of plots with an Axes for each walk\n#grid = sns.FacetGrid(df_stack, col="walk", hue="f", palette="tab20c",\n# col_wrap=4, height=1.5)\n\ngrid = sns.FacetGrid(df_stack, hue="f",\n palette="tab20c", height=1.5)\n\n# Draw a horizontal line to show the starting point\ngrid.refline(y=0, linestyle=":")\n\n# Draw a line plot to show the trajectory of each random walk\ngrid.map(plt.plot, "t", "value", marker="o")\n\n# Adjust the tick positions and labels\ngrid.set(xticks=np.arange(5), yticks=[-3, 3],\n xlim=(-.5, 4.5), ylim=(-3.5, 3.5))\n\n# Adjust the arrangement of the plots\ngrid.fig.tight_layout(w_pad=1)\n\n'
Display using sns.FacetGrid
423 #g = sns.FacetGrid(df_stack, col="f", hue='original')
424 #g.map(sns.swarmplot, "t", "value", alpha=.7)
425 #g.add_legend()
Display using shap.beeswarm
433 # REF: https://github.com/slundberg/shap/blob/master/shap/plots/_beeswarm.py
434 #
435 # .. note: It needs a kernel explainer, and while it works with
436 # common kernels (plot_main07.py) it does not work with
437 # the DeepKernel for some reason (mask related).
Total running time of the script: ( 0 minutes 3.032 seconds)