Note
Go to the end to download the full example code
Using SARIMAX for seasonality
Approximate a function using Sesonal Autoregressive Integrated Moving Average (SARIMA)
Series:
sarimax-aic 765.3684
sarimax-bic 779.585
sarimax-hqic 771.064
sarimax-llf -376.6842
sarimax-intercept_coef 15.1175
...
sarimax-seasonal_order (1, 0, 1, 12)
sarimax-order (0, 1, 1)
sarimax-disp 0
sarimax-model <statsmode...
sarimax-id SARIMAX(0,...
Length: 73, dtype: object
Summary:
SARIMAX Results
==========================================================================================
Dep. Variable: y No. Observations: 80
Model: SARIMAX(0, 1, 1)x(1, 0, 1, 12) Log Likelihood -376.684
Date: Thu, 15 Jun 2023 AIC 765.368
Time: 18:15:49 BIC 779.585
Sample: 0 HQIC 771.064
- 80
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 15.1175 15.426 0.980 0.327 -15.117 45.352
drift -0.2044 0.236 -0.865 0.387 -0.667 0.258
ma.L1 -0.4005 0.097 -4.147 0.000 -0.590 -0.211
ar.S.L12 -0.2805 0.950 -0.295 0.768 -2.142 1.581
ma.S.L12 0.4495 0.873 0.515 0.606 -1.261 2.160
sigma2 804.6743 118.040 6.817 0.000 573.320 1036.028
==============================================================================
Ljung-Box(L1)(Q): 0.32 Jarque-Bera (JB): 14.26
Prob(Q): 0.57 Prob(JB): 0.00
Heteroskedasticity(H): 1.28 Skew: -0.79
Prob(H)(two-sided): 0.53 Kurtosis: 4.36
==============================================================================
Manual
------------------------------------------------------------------------------
Omnibus: 0.000 Durbin-Watson: 2.097
Normal (N): 11.607 Prob(N): 0.003
==============================================================================
Note that JB, P(JB), skew and kurtosis have different values.
Note that Prob(Q) tests no correlation of residuals.
8 # Import.
9 import sys
10 import warnings
11 import pandas as pd
12 import matplotlib as mpl
13 import matplotlib.pyplot as plt
14
15 # Import sarimax
16 from statsmodels.tsa.statespace.sarimax import SARIMAX
17
18 # import weights.
19 from pyamr.datasets.load import make_timeseries
20 from pyamr.core.regression.sarimax import SARIMAXWrapper
21
22 # Filter warnings
23 warnings.simplefilter(action='ignore', category=FutureWarning)
24
25 # ----------------------------
26 # set basic configuration
27 # ----------------------------
28 # Matplotlib options
29 mpl.rc('legend', fontsize=6)
30 mpl.rc('xtick', labelsize=6)
31 mpl.rc('ytick', labelsize=6)
32
33 # Set pandas configuration.
34 pd.set_option('display.max_colwidth', 14)
35 pd.set_option('display.width', 150)
36 pd.set_option('display.precision', 4)
37
38 # ----------------------------
39 # create data
40 # ----------------------------
41 # Create timeseries data
42 x, y, f = make_timeseries()
43
44 # Create exogenous variable
45 exog = x
46
47 # ----------------------------
48 # fit the model
49 # ----------------------------
50 # Create specific sarimax model.
51 sarimax = SARIMAXWrapper(estimator=SARIMAX) \
52 .fit(endog=y[:80], exog=None, trend='ct',
53 seasonal_order=(1, 0, 1, 12), order=(0, 1, 1),
54 disp=0)
55
56 # Print series
57 print("\nSeries:")
58 print(sarimax.as_series())
59
60 # Print summary.
61 print("\nSummary:")
62 print(sarimax.as_summary())
63
64 # -----------------
65 # Save & Load
66 # -----------------
67 # File location
68 # fname = '../../examples/saved/arima-sample.pickle'
69
70 # Save
71 # arima.save(fname=fname)
72
73 # Load
74 # arima = ARIMAWrapper().load(fname=fname)
75
76
77 # -----------------
78 # Predict and plot
79 # -----------------
80 # This example shows how to make predictions using the wrapper which has
81 # been previously fitted. It also demonstrateds how to plot the resulting
82 # data for visualization purposes. It shows two different types of
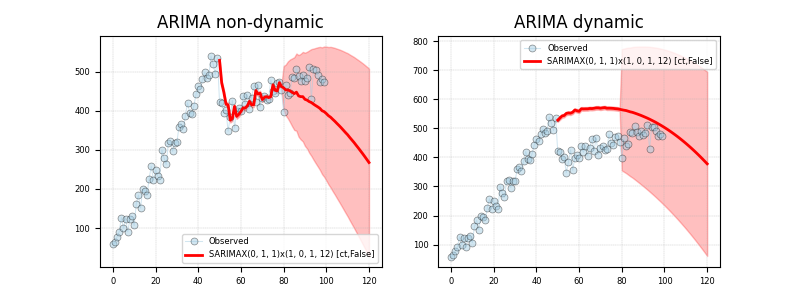
83 # predictions:
84 # - dynamic predictions in which the prediction is done based on the
85 # previously predicted values. Note that for the case of ARIMA(0,1,1)
86 # it returns a line.
87 # - not dynamic in which the prediction is done based on the real
88 # values of the time series, no matter what the prediction was for
89 # those values.
90
91 # Variables.
92 s, e = 50, 120
93
94 # Compute predictions
95 preds_1 = sarimax.get_prediction(start=s, end=e, dynamic=False)
96 preds_2 = sarimax.get_prediction(start=s, end=e, dynamic=True)
97
98 # Create figure
99 fig, axes = plt.subplots(1, 2, figsize=(8, 3))
100
101 # ----------------
102 # Plot non-dynamic
103 # ----------------
104 # Plot truth values.
105 axes[0].plot(y, color='#A6CEE3', alpha=0.5, marker='o',
106 markeredgecolor='k', markeredgewidth=0.5,
107 markersize=5, linewidth=0.75, label='Observed')
108
109 # Plot forecasted values.
110 axes[0].plot(preds_1[0, :], preds_1[1, :], color='#FF0000', alpha=1.00,
111 linewidth=2.0, label=sarimax._identifier())
112
113 # Plot the confidence intervals.
114 axes[0].fill_between(preds_1[0, :], preds_1[2, :],
115 preds_1[3, :],
116 color='#FF0000',
117 alpha=0.25)
118
119 # ------------
120 # Plot dynamic
121 # ------------
122 # Plot truth values.
123 axes[1].plot(y, color='#A6CEE3', alpha=0.5, marker='o',
124 markeredgecolor='k', markeredgewidth=0.5,
125 markersize=5, linewidth=0.75, label='Observed')
126
127 # Plot forecasted values.
128 axes[1].plot(preds_2[0, :], preds_2[1, :], color='#FF0000', alpha=1.00,
129 linewidth=2.0, label=sarimax._identifier())
130
131 # Plot the confidence intervals.
132 axes[1].fill_between(preds_2[0, :], preds_2[2, :],
133 preds_2[3, :],
134 color='#FF0000',
135 alpha=0.25)
136
137 # Configure axes
138 axes[0].set_title("ARIMA non-dynamic")
139 axes[1].set_title("ARIMA dynamic")
140
141 # Format axes
142 axes[0].grid(True, linestyle='--', linewidth=0.25)
143 axes[1].grid(True, linestyle='--', linewidth=0.25)
144
145 # Legend
146 axes[0].legend()
147 axes[1].legend()
148
149 # Show
150 plt.show()
Total running time of the script: ( 0 minutes 0.492 seconds)