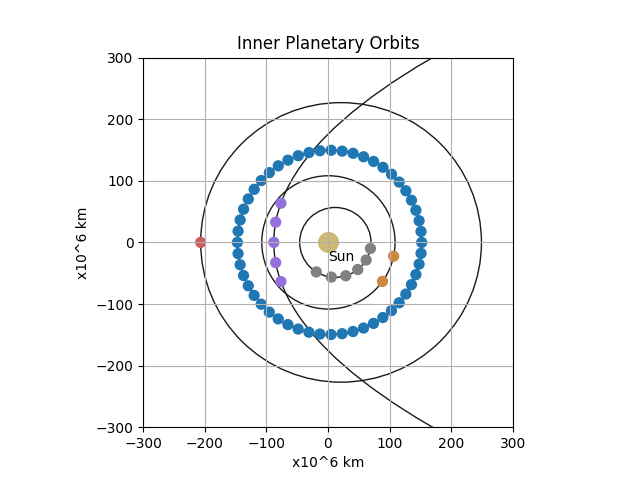
Drawing a planet orbit (customised)

The Wikipedia article describes a method step by step how to calculate the position (in heliocentric polar coordinates) as a function of time. The equations contain Newton’s gravitational constant and the mass of the Sun. Some of them are only solveable by numeric methods.

• R1: Stack Overflow Reference.

• R2: Wikipedia article.

Out:

{'Name': 'Mercury', 'Color': 'grey', 'Aphelion (10^6 km)': 69.8, 'Perihelion (10^6 km)': 46.0, 'Orbital Period (days)': 88, 'Diameter (km)': 4879}
{'Name': 'Venus', 'Color': 'peru', 'Aphelion (10^6 km)': 108.9, 'Perihelion (10^6 km)': 107.5, 'Orbital Period (days)': 224.7, 'Diameter (km)': 12104}
{'Name': 'Earth', 'Color': 'tab:blue', 'Aphelion (10^6 km)': 152.1, 'Perihelion (10^6 km)': 147.1, 'Orbital Period (days)': 365.25, 'Diameter (km)': 12756}
{'Name': 'Mars', 'Color': 'indianred', 'Aphelion (10^6 km)': 249.1, 'Perihelion (10^6 km)': 206.7, 'Orbital Period (days)': 687, 'Diameter (km)': 6792}
{'Name': 'Halley', 'Color': 'mediumpurple', 'Aphelion (10^6 km)': 45900, 'Perihelion (10^6 km)': 88, 'Orbital Period (days)': 246909.0, 'Diameter (km)': 11}

# Libraries
import math
import pandas as pd
import matplotlib.pyplot as plt

from matplotlib.patches import Ellipse
from matplotlib.patches import Circle


EPSILON = 1e-12


# Implementing ellipse equations to generate the values needed to plot an ellipse
# Using only the planet's min (m) and max (M) distances from the sun
# Equations return '2a' (the ellipses width) and '2b' (the ellipses height)
def orbit_length(M, m):
    a = (M + m) / 2
    c = a - m
    e = c / a
    b = a * (1 - e ** 2) ** 0.5
    return 2 * a, 2 * b

def solve_bisection(fn, xmin, xmax, epsilon=EPSILON):
    while True:
        xmid = (xmin + xmax) * 0.5
        if (xmax - xmin < epsilon):
            return xmid
        fn_mid = fn(xmid)
        fn_min = fn(xmin)
        if fn_min * fn_mid < 0:
            xmax = xmid
        else:
            xmin = xmid

def get_planet_coordinates(rmax, rmin, t):
    """Get the planet cartesian coordinates.

    :param rmax:
    :param rmin:
    :param t:
    :return:
    """
    SCALE = 1e9
    theta, r = get_planet_solve_orbit(rmax * SCALE, rmin * SCALE, t)
    x = -r * math.cos(theta) / SCALE
    y = r * math.sin(theta) / SCALE
    return x, y

def get_planet_solve_orbit(rmax, rmin, t):
    """Get the planet orbit parameters

    .. note:: Polar coordinates.

    :param rmax:
    :param rmin:
    :param t:
    :return:
    """
    # calculation precision
    epsilon = EPSILON
    # mass of the sun [kg]
    Msun = 1.9891e30
    # Newton's gravitational constant [N*m**2/kg**2]
    G = 6.6740831e-11
    # standard gravitational parameter
    mu = G * Msun
    # eccentricity
    eps = (rmax - rmin) / (rmax + rmin)
    # semi-latus rectum
    p = rmin * (1 + eps)
    # semi/half major axis
    a = p / (1 - eps ** 2)
    # period
    P = math.sqrt(a ** 3 / mu)
    # mean anomaly
    M = (t / P) % (2 * math.pi)

    # eccentric anomaly
    def fn_E(E):
        return M - (E - eps * math.sin(E))

    E = solve_bisection(fn_E, 0, 2 * math.pi)
    # true anomaly
    # TODO: what if E == pi?
    theta = 2 * math.atan(math.sqrt((((1 + eps) * math.tan(E / 2) ** 2) / (1 - eps))))
    # if we are at the second half of the orbit
    if (E > math.pi):
        theta = 2 * math.pi - theta
    # heliocentric distance
    r = a * (1 - eps * math.cos(E))
    return theta, r

def get_planet_orbit(M, m):
    """

    :param M:
    :param m:
    :return:
    """
    w, h = orbit_length(M, m)
    Xoffset = ((M + m) / 2) - m
    return w, h, Xoffset

def plot_orbit(d, ax, **kwargs):
    """Plot the orbit.

    :param d:
    :param kwargs:
    :return:
    """
    # Dictionary
    print(d)
    M = d.get('Aphelion (10^6 km)')
    m = d.get('Perihelion (10^6 km)')

    # Create planet orbit (ellipse)
    w, h, x_offset = get_planet_orbit(M, m)
    orbit = Ellipse(xy=((x_offset), 0), width=w, height=h,
                    angle=0, linewidth=1, fill=False,
                    color='k')

    # Draw
    ax.add_artist(orbit)

def plot_planet(d, ax, start=0, stop=1, coeff=1, size=None):
    """Plot the planet.

    .. note: We could include sizes, but because the diameters
             vary considerably, some of them might not be
             visible and would need to be re-scaled.

    Params
    ------

    """
    M = d.get('Aphelion (10^6 km)')
    m = d.get('Perihelion (10^6 km)')
    #p = d.get('Orbital Period (days)')
    #s = d.get('Diameter (km)') if size is None else size

    for i in range(start, stop):
        t = i * coeff * 60 * 60 * 24
        x, y = get_planet_coordinates(M, m, t)
        planet = Circle((x, y), 8, color=d.get('Color'))
        ax.add_artist(planet)



# ---------------------------------------
# Main
# ---------------------------------------
# Information of the planets in a list format.
PLANETS = [
    {
        'Name': 'Mercury',
        'Color': 'grey',
        'Aphelion (10^6 km)': 69.8,
        'Perihelion (10^6 km)': 46.0,
        'Orbital Period (days)': 88,
        'Diameter (km)': 4879
    },
    {
        'Name': 'Venus',
        'Color': 'peru',
        'Aphelion (10^6 km)': 108.9,
        'Perihelion (10^6 km)': 107.5,
        'Orbital Period (days)': 224.7,
        'Diameter (km)': 12104
    },
    {
        'Name': 'Earth',
        'Color': 'tab:blue',
        'Aphelion (10^6 km)': 152.1,
        'Perihelion (10^6 km)': 147.1,
        'Orbital Period (days)': 365.25,
        'Diameter (km)': 12756
    },
    {
        'Name': 'Mars',
        'Color': 'indianred',
        'Aphelion (10^6 km)': 249.1,
        'Perihelion (10^6 km)': 206.7,
        'Orbital Period (days)': 687,
        'Diameter (km)': 6792
    },
    {
        'Name': 'Halley', # commet
        'Color': 'mediumpurple',
        'Aphelion (10^6 km)': 45900,
        'Perihelion (10^6 km)': 88,
        'Orbital Period (days)': 676 * 365.25,
        'Diameter (km)': 11
    }
]

# Load planet information from .csv file
#PLANETS = pd.read_csv('./data/orbits.csv') \
#    .to_dict(orient='records')

# Information of the planets in a dict format where
# the key is the name and the value is the full object.
PLANETS_DICT = { e.get('Name'): e for e in PLANETS }

# Create figure. Set axes aspect to equal as orbits are
# almost circular; hence square is needed
ax = plt.figure(1).add_subplot(111, aspect='equal')


# ---------------------------------------
# Draw orbits
# ---------------------------------------
# Drawing orbits
for n in PLANETS_DICT.keys():
    plot_orbit(PLANETS_DICT.get(n), ax)


# ---------------------------------------
# Draw planets
# ---------------------------------------
#
# .. note:: The coefficient broadly indicates in how many portions
#           to divide the orbit. Then you will plot one marker for
#           each of the elements within start and stop.
#
# Plot planets at different t.
plot_planet(PLANETS_DICT.get('Mercury'), ax, start=8, stop=14, coeff=1/15*88)
plot_planet(PLANETS_DICT.get('Venus'), ax, start=8, stop=10, coeff=1/15*224.7)
plot_planet(PLANETS_DICT.get('Earth'), ax, start=0, stop=52, coeff=1/52*365.25)
plot_planet(PLANETS_DICT.get('Mars'), ax, start=0, stop=1, coeff=1/4*687)
plot_planet(PLANETS_DICT.get('Halley'), ax, start=-2, stop=3, coeff=7)

# Axis configuration
plt.title('Inner Planetary Orbits')
plt.ylabel('x10^6 km')
plt.xlabel('x10^6 km')
ax.set_xlim(-300, 300)
ax.set_ylim(-300, 300)
plt.grid()

# Creating the point to represent the sun at the origin (not to scale),
ax.scatter(0, 0, s=200, color='y')
plt.annotate('Sun', xy=(0, -30))

# Show
plt.show()